ГЛАВА
3.
Представление
знаний
В этой
главе...
В главе 2
отмечалось, что большинство исследователей весьма скептически относятся к возможности
использования в прикладных системах таких методик поиска решений проблем, как
"порождение и проверка" и "восхождение на гору". Серьезные
технические сложности программной реализации оценочных функций навели на мысль,
что такая методика недооценивает возможности узкоспециальных знаний в конкретной
предметной области и переоценивает возможности обобщенного подхода к воспроизведению
механизмов человеческого мышления. Весьма мало вероятно, что сегодня существовала
бы такая область исследований, как экспертные системы, если бы удалось найти
общие принципы решения проблем, которые можно было применять, отвлекаясь от
специфики конкретной предметной области.
В этой главе
описана одна из первых экспертных систем, MYCIN, при разработке которой была
предпринята попытка отойти от традиции использования "обобщенного решателя
проблем". Система построена на основе относительно несложного алгоритма
поиска, значительно более простого, чем описанный в предыдущей главе алгоритм
А. Возможности программы определяются не столько реализованным в ней алгоритмом
поиска, сколько методикой представления знаний, специфических для той области,
в которой предполагалось использовать систему, а именно — в лечении заболеваний
крови.
Но начнем
мы с разъяснения таинственного термина "представление знаний", используя
в качестве примера разработанную приблизительно в это же время другую программу
искусственного интеллекта — программу планирования STRIPS, — которую еще нельзя
было отнести к классу экспертных систем. Затем будет описана система MYCIN,
использованные в ней средства представления знаний и алгоритмы. Будет показано,
как в процессе эксплуатации совершенствовалась система и с помощью каких средств
разработчики пытались повысить ее производительность. В заключение мы сравним
обе системы и отметим, что есть в них общего и в чем существенная разница. Анализ
отличий между системами поможет проиллюстрировать тот существенный вклад, который
внесли разработчики ранних экспертных систем в теорию и практику искусственного
интеллекта в начале 70-х годов.
3.1.
Представление знаний: принципы и методы
В области
экспертных систем представление знаний означает не что иное, как систематизированную
методику описания на машинном уровне того, что знает человек-эксперт, специализирующийся
в конкретной предметной области. Но ошибочно считать, будто представление знаний
сводится к кодированию в смысле, аналогичном шифрованию. Если закодировать сообщение,
подставив некоторым регулярным образом вместо одних символов другие, то полученный
результат не имеет ничего общего с представлением содержания сообщения
в том смысле, как это понимается в теории искусственного интеллекта, даже если
полученный код легко воспринимается на машинном уровне и его можно хранить в
памяти компьютера.
Обратим внимание
хотя бы на то, что в таком коде сохраняется та лексическая или структурная неоднозначность,
которая присуща естественному человеческому языку. Так, сообщение
"Посещение
тетушки может быть надоедливым"
будет настолько
же неоднозначным в кодированном виде, что и на "человеческом" языке.
Перевод этого текста в машинный код не избавит нас от того, что это сообщение
можно трактовать и как утверждение, что "надоедает наносить визиты тетушке",
и как утверждение, что "надоедает, когда тетушка наносит визит".
3.1. Молотки,
графины и теоремы
Один из
парадоксов искусственного интеллекта состоит в том, что многие задачи поиска
смыслового содержания, которые легко решаются человеком, очень трудно реализовать
на машине и наоборот. Рассмотрим следующую фразу:
"Молоток
ударил графин, и он разбился".
К чему
относится "он" в этой фразе? Для нас ответ очевиден, и мы даже не
замечаем неоднозначности в этой фразе. Но как в общем смысле машина будет интерпретировать
эту фразу? Предположение, что "он" относится к последнему по порядку
следования в предложении существительному, не всегда срабатывает. Например:
Графин
ударился о камень, и он разбился."
Для нас
совершенно очевидно, что пострадавшим в обоих случаях должен быть графин. Мы
обладаем тем, что называется "предварительным знанием", но непотнятно,
как оно должно быть представлено в машине. Также далеко не очевидно, как собрать
такого рода знания и как организовать их извлечение в конкретной ситуации. Единственное,
что в этом смысле можно предложить — сформировать огромную таблицу, состоящую
из всевозможных пар объектов во вселенной, и указать в ней, какой из двух предметов
более хрупкий?
Теперь
рассмотрим задачу из совершенно другой области. Нужно решить, является ли некоторая
логическая формула теоремой исчисления высказываний (см. главу 8). Например,
является ли теоремой формула
(р &
(q=>r)) э ((s v p) & (~r=>-q)).
Оказывается,
что не является, поскольку существует вариант, когда истинное значение присваивается
последовательно переменным р, q, r, s, и все выражение становится ложным. Написать
программу, которая поможет компьютеру прийти к такому заключению, — задача довольно
тривиальная, а сделать то же самое обычному человеку довольно сложно.
Грубо
говоря, разница между этими двумя задачами состоит в том, что знание, необходимое
для решения задач из области исчисления высказываний, можно выразить в компактной
форме в виде правил, а знания, которые требуются для правильной интерпретации
любой фразы в форме
"X
ударил Y, и он разбился",
кажутся
на первый взгляд бесконечными по объему и предполагают множество исключений
вроде того, что существует и пластиковый молоток, и выточенная из камня ваза,
бумажная стена и т.д. и т.п. Кажется, что для решения подобных проблем программа
должна обладать чем-то вроде "здравого смысла", в то время как для
решения формальных логических задач никакого здравого смысла не нужно.
Любое
общение человека с миром техники предполагает наличие некоторого предварительного
знания. Если, например, некто берется за поиск неисправности в цифровой схеме,
то это предполагает, что он обладает определенными базовыми знаниями из области
электротехники. Нет необходимости подчеркивать, что компьютер (в чистом виде)
никакими предварительными знаниями не обладает, а потому техническая эксперт-ность
— набор качеств, лежащих в основе высокого уровня работы людей-специалистов
при решении проблем в определенной узкой области, — должна включать и эти предварительные
знания.
И наконец,
представление предполагает определенную организованность знаний. Представление
знаний должно позволить извлекать их в нужной ситуации с помощью относительно
несложного и более-менее естественного механизма. Простого перевода информации
(знаний) в форму, пригодную для хранения на машинных носителях, здесь явно недостаточно.
Для того чтобы можно было достаточно быстро извлекать те элементы знаний, которые
наиболее пригодны в конкретной ситуации, база знаний должна обладать достаточно
развитыми средствами индексирования и контекстной адресации. Тогда программа,
использующая знания, сможет управлять последовательностью применения определенных
"элементов" знания, даже не обладая точной информацией о том, как
они хранятся.
Конечно,
программный код, выполняемый компьютером, должен соответствовать применяемой
системе обозначений, но это нельзя считать слишком уж серьезным ограничением.
Многие схемы представления, на первый взгляд чрезвычайно сильно отличающиеся,
оказываются на самом деле формально эквивалентными, т.е. все, что может быть
выражено в одной системе представления, может быть выражено и в другой.
Прежде
чем перейти к рассмотрению конкретных примеров, давайте уточним терминологию,
взяв за основу цитаты из "классических" работ по искусственному интеллекту.
Представление
(representation) в работе Уинстона [Winston, 1984] определяется как
"множество синтаксических и семантических соглашений, которое делает возможным
описание предмета". В искусственном интеллекте под "предметом"
понимается состояние в некоторой проблемной области, например объекты в этой
области, их свойства, отношения, которые существуют между объектами. Описание
(description) "позволяет использовать соглашения из представления для
описания определенных предметов" [Winston, 1992].
Синтаксис
представления специфицирует набор правил, регламентирующих объединение символов
для формирования выражений на языке представления. Можно говорить о том, что
выражение хорошо или плохо сформировано, т.е. о том, насколько оно соответствует
этим правилам. Смысл должны иметь только хорошо сформированные выражения.
Общепринятым
в области искусственного интеллекта является синтаксис в виде конструкции предикат-аргумент,
которая имеет форму
<фраза>
::= <предикат> (<аргумент>,..., <аргумент>)
В этой конструкции
за к-местным предикатом должны следовать k аргументов. Так, at может
быть двухместным отношением, в котором в качестве первого аргумента выступает
имя некоторого объекта, а в качестве второго— его местонахождение (например,
комната):
at(робот,
комнатаА)
Семантика
представления специфицирует, как должно интерпретироваться выражение, построенное
в соответствии с синтаксическими правилами, т.е. как из его фор"мы можно
извлечь какой-то смысл. Спецификация обычно выполняется присвоением смысла отдельным
символам, а затем индуцированием присвоения в более сложных выражениях. Так,
присваивая смысл символам at, робот, комнатаА, мы можем сказать, что выражение
at(робот,
комнатаА)
означает:
робот находится в комнате А (но не наоборот — комната А находится в роботе).
Процесс решение
проблемы, как правило, включает в себя наряду с представлением предметов окружающего
мира и суждение о некоторых действиях. Как уже было показано в главе 2, некоторые
проблемы формулируются в терминах исходного и целевого состояний и множества
операций, которые можно использовать при попытках преобразовать начальное состояние
в целевое. Но здесь остается невыясненным вопрос о том, как можно представлять
операции.
Программа
STRIPS [Fikes and Nilsson, 1971] демонстрирует один из подходов к представлению
проблем. Наименование программы — аббревиатура от Stanford Research Institute
Problem Solver (решатель проблем Станфордского исследовательского института).
Программа предназначалась для решения проблемы формирования плана поведения
робота, перемещающего предметы через множество (анфиладу) помещений. Программа
STRIPS оказала очень большое влияние на последующие разработки в области искусственного
интеллекта, и те базовые методики представления знаний, которые были в ней использованы
для формирования действий, не утратили своей актуальности до настоящего времени.
Текущее состояние
окружающей среды — помещений и предметов в них — представляется набором выражений
предикат-аргумент, которые в совокупности образуют модель мира. Так,
набор формул
W = { at(po6oт,
комнатаА), at(ящик1, комнатаБ), at(ящик2, комнатаВ)}
означает,
что робот находится в комнате А и имеются два ящика, один из которых находится
в комнате Б, а второй — в комнате В.
Действия,
которые может выполнить робот, принимают форму операторов, приложимых к текущей
модели мира. Эти операторы позволяют добавить в модель некоторые факты (сведения)
или изъять их из модели. Например, выполнение операции
"Переместить
робот из комнаты А в комнату Б"
в модели
мира приведет к формированию новой модели W. При этом факт at (робот,
комнатаА) будет изъят из модели, а добавлен факт at (робот, комнатаБ). В результате
новая модель мира будет иметь вид
W' = { at
(робот, комнатаБ), at (ящик1, комнатаБ), аt (ящик2, комнатаВ)}
Обращаю ваше
внимание на то, что сейчас мы обсуждаем только символические преобразования
в модели мира и не затрагиваем вопрос о возможности реального перемещения робота
из комнаты А в комнату Б. Обладающий интеллектом робот должен быть не только
способен изменять свое реальное положение в окружающей среде, но и одновременно
менять свое внутренне представление этой среды, знать, где он сейчас находится.
3.2.1.
Таблицы операторов и методика "средство -анализ завершения"
Допустимые
операции, такие как перемещение робота из одной комнаты в другую или проталкивание
объектов, кодируются в таблице операторов. Ниже показан элемент этой
таблицы, соответствующий операции push (толкать):
push(X, Y, Z)
Предварительные
условия at(po6oT, Y), at(X, Y)
Список удалений
at (робот, Y), at(X, Y)
Список добавлений
at (робот, Z), at(X, Z)
Здесь выражение
push(X, Y, Z)
означает,
что объект X выталкивается (роботом) из положения Y в положение
Z, причем X, Y и Z — переменные в области значений, охватывающей
доступное множество объектов, в то время как робот, комнатаА, ящик1, комнатаБ,
ящик2, комнатаВ — это имена конкретных объектов из этого множества.
С точки зрения
программиста переменные X, К и Z в определении оператора, заданном элементом
таблицы, — это аналоги формальных параметров в определении процедуры, которая
соответствует такому действию:
"Вытолкнуть
какой-либо объект из какого-либо положения в любое другое положение, если имеют
место заданные предварительные условия; затем удалить формулы, указанные в списке
удаления, и добавить формулы, указанные в списке добавления".
С точки зрения
логики элемент push таблицы операторов может быть прочитан в виде формулы, которая
утверждает:
"При
любых X, Y и Z объект X выталкивается из Y в Z, если робот и объект
X находятся в 7, а затем состояние изменятся заменой Y на Z".
Целевое состояние
также представляется формулой, например: а1(ящик1, комнатаА), а^ящик2, комнатаБ).
Программа
STRIPS включает множество процедур, которые выполняют различные функции, в частности:
Чтобы представить
себе, как на практике использовать подобную "структуру представлений, рассмотрим
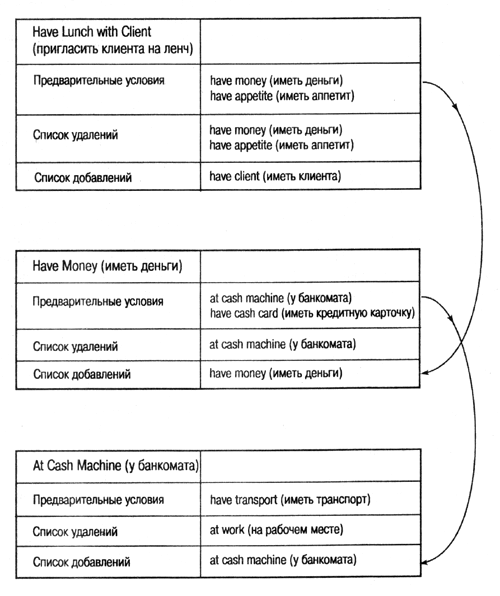
простую задачу: как готовиться к ленчу с потенциальным клиентом. Для этого,
во-первых, нужно иметь в своем распоряжении определенную сумму наличных денег,
чтобы расплатиться, во-вторых, нужно проголодаться, поскольку речь идет о приеме
пищи. Сформулированные условия можно рассматривать в качестве предварительных
для достижения цели "ленч". Эта цель может быть представлена оператором,
как на рис. 3.1. После завершения ленча деньги будут потрачены, а у вас исчезнет
чувство голода. Эти простые факты нашли отражение в списках удалений и добавлений
для оператора have lanch. Однако обладание известной суммой наличных денег нельзя
рассматривать как естественное состояние клиента. Сначала нужно получить их
в банкомате, что, в свою очередь, требует передвижения. Следовательно, нужно
добавить в таблицу операторов еще два элемента — at cash mashine (передвижение
к банкомату) и have money (получение наличности).
Этот простой
пример обладает довольно интересными свойствами. Отметим, что формулы для модели
мира в исходном состоянии
at(work), have(transport)
остаются
в неприкосновенности до тех пор, пока мы явно не удалим их. Таким образом, у
вас остается возможность передвигаться по городу на протяжении всего времени
реализации плана, поскольку формально отсутствуют какие-либо признаки, что эта
возможность может быть утеряна (например, автомобиль будет угнан, или вы попадете
в дорожную аварию, или по дороге к банкомату кончится бензин). Точно так же
может что-нибудь произойти и с банкоматом — он может "зажевать" карточку,
или вы можете забыть вытащить ее, или может вдруг появиться механическая рука
и ножницами разрезать ее. Но предполагается, что последовательность действий,
представленная в сгенерированном машиной плане, не должна предвидеть такие исключительные
ситуации, хотя в реальной обстановке это соблюдается далеко не всегда.
Такая стратегия
"обратных" рассуждений, т.е. от целей к подцелям, чрезвычайно распространена
в программах искусственного интеллекта и экспертных системах, как вы вскоре
убедитесь на примере системы MYCIN. Но даже на таком ограниченном множестве
операторов, как в нашем примере, может существовать несколько вариантов выполнения
действий. В этом случае необходимо будет организовать какой-то механизм поиска
наилучшей последовательности операторов, приводящих к достижению сформулированной
цели.

Рис. 3.1.
Таблица операторов для задачи "Ленч"
По существу,
в системе STRIPS при выборе операторов выполняется поиск в пространстве состояний,
как это было описано в главе 2. В результате формируется план, т.е. последовательность
операторов, приводящая к достижению цели, причем за основу берется стратегия
"обратного" прослеживания. Основное отличие STRIPS от других аналогичных
программ состоит в том, что вместо методики "генерация —проверка"
для передвижения в пространстве состояний используется другой метод, известный
как "средство — анализ завершения" (means-ends analisys).
В контексте
нашей задачи применение методики "генерация —проверка" означает следующее:
для каждого текущего состояния предпринимаются попытки использовать все возможные
операторы, причем после каждой попытки анализируется, не привела ли она к желанной
цели. Но такая методика явно бессмысленна, поскольку количество разнообразных
операций, которые робот способен выполнить в некоторой произвольной ситуации,
очень велико, причем многие из этих операций не имеют никакого отношения к достижению
заданной цели. Уже после нескольких первых испытаний размерность пространства
состояний увеличится и будет экспоненциально нарастать с каждым новым испытанием.
Совершенно очевидно, что в данном случае нужна совершенно иная стратегия.
Основная
идея, которая лежит в основе метода "средство — анализ завершения",
состоит в том, чтобы с каждой новой операцией отличие между текущим состоянием
и целевым уменьшалось, т.е. каждая очередная операция должна приближать нас
к цели. Но это предполагает включение в рассмотрение некоторой меры для оценки
"расстояния" в пространстве состояний. Такая мера очень походит на
оценочную функцию. Если очередная цель сформулирована в виде
at(ящик1, комнатаА),
а ящик находится
в комнате Б, то перемещение робота из комнаты А в комнату В никак не "приблизит"
текущее состояние к целевому. А вот перемещение робота из комнаты А в комнату
Б уменьшит расстояние между текущим и целевым состоянием, поскольку робот теперь
сможет на очередном шаге вытолкнуть ящик из комнаты Б в комнату А. В этом смысле
поведение робота "мотивируется" от целевого состояния к подцелям,
которые могут привести к достижению сформулированной цели.
В действительности
программа STRIPS считывает список целей наподобие такого:
at(ящик1, комнатаА),
аt(ящик2, комнатаБ),
а затем сопоставляет
эти цели и список добавления в описании каждого оператора. Так, цель at (ящик!,
комнатаА) будет соответствовать элементу at(X, Z) в списке добавлений оператора
push (X, Y, Z).
Схема сопоставления
будет подробно рассмотрена в главах 4, 5 и 8, но сейчас, не вдаваясь в детали,
просто отметим, что существует подстановка значений переменных
Х/ящик1, Z/комнатаА,
которая приводит
к равенству выражений at (ящик!, комнатаА) nat(X, Z).
Программа
следующим образом формирует подцели, выбирая в качестве таковых предварительные
условия оператора.
(1) Подстановкой
{Х/ящик1, Z/комнатаА} означить предварительное условие, которое является
производным от соответствия at (ящик!, комнатаА) nat(X, Z), и получить таким
образом
at(po6oт
, Y), at(ящик1, Y).
(2) Найти
в модели мира формулу, которая представляла бы текущее положение ящика а1(ящик1,
комнатаБ), сравнить ее с at(ящик1, Y) и в результате этого сравнения сформулировать
подстановку {Y/комнатаБ}, которую затем применить к уже частично означенному
предварительному условию. В результате будет сформулирована очередная подцель:
at(робот, комнатаБ),
at(ящик1, комнатаБ).
Теперь первое
предварительное условие даст желаемое (целевое) положение робота, а второе предварительное
условие уже выполнено.
Так как таблица
операторов, модель мира и цели представлены с помощью одного и того же синтаксиса
в виде конструкций предикат-аргумент, то, применяя описанную выше схему
сопоставления, программа довольно просто находит, какие именно операции нужно
выполнить для достижения поставленной цели. Все, что нужно для этого сделать,
— просмотреть списки добавлений в описании операторов и найти в них элемент,
соответствующий заданной цели, как это показано на рис. 3.1.
Подцели формулируются
на основе анализа предварительных условий, заданных для операторов, означивая
их подстановкой переменных из формулы модели мира. Как только выбран нужный
оператор, его предварительные условия преобразуются и добавляются в список подцелей.
Если в текущем состоянии можно применить не один оператор, то для выбора между
"кандидатами" нужно применить какую-либо эвристику. Например, можно
выбрать тот из операторов, который сулит наибольшее сокращение "расстояния"
между текущим состоянием и целевым. Другой возможный вариант — операторы в таблице
заранее упорядочены и нужно применять тот из них, который стоит в списке раньше.
Весь процесс
решения проблемы по такой методике имеет ярко выраженный рекурсивный характер.
Подцели могут, в свою очередь, приводить к формулировке подподце-лей и т.д.
На самом нижнем уровне окажутся подцели, которые реализуются операторами, либо
не имеющими предварительных условий, либо имеющими такие предварительные условия,
которые удовлетворяются тривиально. Мы рассмотрим подробно методику "средство
— анализ завершения" в главах 5 и 14.
3.2.2.
Анализ метода представления и управления в STRIPS
Для того
чтобы яснее представить себе достоинства метода представления, использованного
в системе STRIPS, рассмотрим альтернативный метод. Предположим, что текущее
состояние окружающего мира представлено в виде двумерного массива с элементами
разного размера (в таком массиве элементы верхнего уровня — ячейки — представляют
различные помещения, а элементы второго уровня — объекты в этих помещениях).
Такой вариант представления компактнее описательного, но он не позволяет выполнять
операции сопоставления, описанные в предыдущем разделе. Можно, конечно, придумать
какой-нибудь способ описания целей и операций на языке, ориентированном на работу
с массивами, но тогда будут утеряны некоторые из главных достоинств рассмотренной
методики.
стояние мира,
а множество состояний, удовлетворяющих сформулированному условию. При такой
постановке проблемы набор процедур, ориентированных на табличное представление,
придется пересмотреть коренным образом. Представление на базе конструкций предикат-аргумент
позволяет выразить целевое состояние, введя в выражение переменные
at(X, комнатаА),
at(Y, комнатаА), at(Z, комнатаА).
После этого
можно использовать прежнюю методику поиска решения.
Язык представления,
подобный тому, что используется в STRIPS, с точки зрения программной реализации
является интерпретируемым языком, т.е. трансляция с этого языка выполняется
интерпретатором, программой, которая способна распознавать в операторах языка
формулы, подобные рush(ящик1, комнатаБ, комнатаА), и выразить заложенный в формулах
смысл в терминах выполняемых процедур. Так, смысл приведенной выше формулы интерпретируется
как необходимость достичь предварительных условий
at(робот, комнатаБ),
at(ящик1, комнатаБ),
а затем реализовать
действия, предписанные списками добавлений и исключений, т.е. добавить в модель
мира состояние
at(po6oт, комнатаА), at(ящик1, комнатаА)
и исключить
из модели мира состояние
at(робот, комнатаБ),
at(ящик1, комнатаБ).
Такой подход
к интерпретации получил наименование проиедуральной семантики (procedural
semantics), поскольку все, что известно программе о смысле формулы, — какие
действия ей нужно выполнить для того, чтобы формула получила значение Истина.
Как отмечалось в главе 2, это не очень широкое толкование смысла, и такой
подход вряд ля продвинет нас далеко в развитии машинного "понимания".
Но, тем не менее, процедуральная семантика позволяет нам по крайней мере построить
связь между мыслью и действием.
3.3.
Формулировка подцелей в MYGIN
По сравнению
с STRIPTS, программа MYCIN менее однородна и включает в свой состав множество
различных модулей. Однако в структуре управления программой MYCIN можно найти
элементы, в определенной мере схожие с элементами STRIPS. Это, в частности,
относится к той части программы, которая реализует квазидиагностическую функцию.
Правда, цель, которая должна быть достигнута в этом случае, является не физическим
состоянием, а некоторым суждением, предполагающим формулировку диагностических
гипотез.
В этом разделе
основное внимание будет уделено диагностическому модулю MYCIN. Мы дадим несколько
упрощенное описание его назначения, структуры и функционирования в процессе
эксплуатации системы. Затем мы проведем сравнительный анализ работы модуля диагностирования
MYCIN и работы STRIPTS, особо останавливаясь на тех качественных отличиях, которые
существуют между классом экспертных систем, к которым принадлежит MYCIN, и классом
исследовательских программ искусственного интеллекта, к которым относится STRIPTS.
В конце этой главы мы кратко остановимся на эволюции экспертных систем, а затем
вновь вернемся к этому вопросу в главе 14.
3.3.1.
Лечение заболеваний крови
Сначала нам
предстоит небольшой экскурс в ту предметную область, в которой используется
MYCIN, — в область диагностики и лечения заболеваний крови. Это описание достаточно
поверхностное, поскольку рассчитано на читателей, не имеющих специальных познаний
в медицине. Но, как мы уже не раз подчеркивали, нельзя рассматривать структуру
и работу экспертной системы в отрыве от той предметной области, с которой данная
система имеет дело.
"Антимикробный
агент"— это любой лекарственный препарат, созданный для уничтожения бактерий
и воспрепятствования их роста. Некоторые агенты слишком токсичны для терапевтических
целей, и не существует агента, который является эффективным средством борьбы
с любыми бактериями. Выбор терапии при бактериальном заражении состоит из четырех
этапов:
Первичные
анализы, взятые у пациента, направляют в микробиологическую лабораторию, где
из них выращивается культура бактерий, т.е. создаются наилучшие условия для
их роста. Иногда уже на ранних стадиях можно сделать заключение о морфологических
характеристиках микроорганизмов. Но даже если микроорганизм, вызвавший заражение,
и идентифицирован, еще неизвестно (или нет полной уверенности), к каким препаратам
он чувствителен.
Часто программу
MYCIN считают диагностической, но это не так. Назначение этой программы — быть
ассистентом врача, который не является узким специалистом в области
применения антибиотиков при лечении заболеваний крови. В процессе работы программа
формирует гипотезы диагноза и придает им определенные веса, но самостоятельно,
как правило, не делает окончательного выбора. Работа над программой началась
в 1972 году в Станфордеком университете и велась специалистами в области искусственного
интеллекта в тесном сотрудничестве с медиками. Наиболее полное описание этой
системы читатель найдет в работе Шортлиффа [Shortliffe, 1976].
После 1976
года система неоднократно модифицировалась и обновлялась, но базовая версия
состояла из пяти компонентов (рис. 3.2). Стрелки на рисунке показывают основные
потоки информации между модулями.
(1) База
знаний содержит фактические знания, касающиеся предметной области, и сведения
об имеющихся неопределенностях.
(2) Динамическая
база данных пациентов содержит информацию о конкретных пациентах и их заболеваниях.
(3) Консультирующая
программа задает вопросы, выводит заключения системы и дает советы для конкретного
случая, используя информацию о пациенте и статические знания.
(4) Объясняющая
программа отвечает на вопросы и дает пользователю информацию о том, на чем
основываются рекомендации или заключения, сформулированные системой. При этом
программа приводит трассировку процесса выработки рекомендаций.
(5) Программа
восприятия знаний служит для обновления знаний, хранящихся в системе, в
процессе ее эксплуатации.
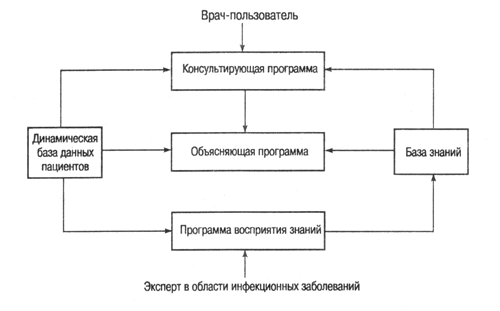
Рис. 3.2.
Структура системы MYC1N ([Buchanan and Shortliffe, 1984])
Подсистема,
в которую входят компоненты 1, 2 и 3, отвечает за решение проблемы. Эта подсистема
строит гипотезы относительно причин заболевания и формирует рекомендации, основываясь
на этих гипотезах. Ниже мы подробнее рассмотрим принципы работы этих компонентов.
Методы восприятия знаний, в частности и те, которые использованы в компоненте
системы MYCIN, мы рассмотрим в главах 10-15, а работа объясняющей программы
будет описана в главе 16.
3.3.2.
База знаний системы MYCIN
База знаний
системы MYCIN организована в виде множества правил в форме если
условие1 и... и условиет удовлетворяются то прийти
к заключению1 и... и к заключению n
Эти правила
преобразованы в операторы языка LISP (подробнее о программировании базы знаний
рассказано в главе 4).
Вот как выглядит
перевод на обычный язык типичного правила MYCIN:
ЕСЛИ 1) организм
обладает грамотрицательной окраской, и
2) организм
имеет форму палочки, и
3) организм
аэробный,
ТО есть основания
предполагать (0,8), что этот микроорганизм относится к классу enterobacteriaceae.
Такого рода
правила названы оргправилами (ORGRULES) и в них сконцентрированы знания
о таких организмах, как strepococcus , pseudonomas и enterobacteriaceae.
Это правило
говорит о том, что если организм имеет форму палочки, пятнистую окраску и активно
развивается в среде, насыщенной кислородом, то с большой вероятностью его можно
отнести в классу enterobacteriaceae. Число 0.8 называется уровнем
соответствия (tally) правила, т.е. мерой правдоподобия заключения, сделанного
на основании сформулированных условий. Методика использования уровня соответствия
правила будет рассмотрена ниже. Каждое правило такого вида можно рассматривать
как представление в машинной форме некоторого элемента знаний эксперта. Возможность
применить правило определяется тем, удовлетворяются ли в конкретной ситуации
условия, сформулированные в первой его части. Сформулированные условия также
носят нечеткий характер и могут удовлетворяться с разной степенью истинности.
Поэтому в результате импортирования правил из базы знаний применительно к конкретной
ситуации формируется более общее правило, включающее и оценки уровня истинности
соблюдения условий:
если условие1
удовлетворяется с истинностью х1 и ... и условиеm удовлетворяется
с истинностью хм,
то прийти
к заключению1 со степенью уверенности у1 и
... и к заключениюn со степенью уверенности уn.
Здесь степень
уверенности, связанная с каждым заключением, является функцией от оценок истинности
соблюдения условий и уровня соответствия, отражающего степень уверенности эксперта
при формулировке первичных оргправил.
Фактически
правило является парой "предпосылка—действие"; такое правило иногда
традиционно называют "продукцией" (подробнее об этом см. в главе 5).
Предпосылка — это совокупность условий, а уверенность в достоверности
предпосылки зависит от того, насколько достоверной является оценка условий.
Условия — это предположения о наличии некоторых свойств, которые принимают
значения истина либо
ложь с
определенной степенью достоверности. Примером может служить условие в приведенном
выше правиле:
"Организм
имеет форму палочки".
Действие
— это либо заключение, либо рекомендация о том, какое действие
предпринять. Примером заключения может служить вывод о том, что данный организм
относится к определенному классу. Пример рекомендации — сформулированный перечень
лечебных процедур.
Мы детально
проанализируем процесс применения правил в последующих разделах. А сейчас кратко
остановимся на том, как в MYCIN для представления знаний используются структуры
другого вида.
Помимо правил,
в базе знаний MYCIN также хранятся факты и определения. Для их
хранения используются разные структурные формы:
Значительная
часть знаний хранится не в виде правил, а в виде свойств, ассоциированных с
65 клиническими параметрами, известными системе MYCIN. Например, форма—
это атрибут микроорганизма, который может принимать самые разнообразные значения,
например "палочка" или "кокон". Система также присваивает
значения параметрам и для собственных нужд — либо для упрощения мониторинга
взаимодействия с пользователем, либо для индексации при определении порядка
применения правил.
Информация
о пациенте хранится в структуре, названной контекстным деревом (context tree).
На рис. 3.3 показано контекстное дерево пациента ПАЦИЕНТ 1. В это дерево
включены три культуры организмов (например, полученные из анализа крови пациента)
и текущие назначения, которые нужно учитывать при анализе, поскольку они сопряжены
с приемом определенных лекарственных средств. С культурами связаны микроорганизмы,
присутствие которых предполагается на основании данных, полученных в лаборатории,
а с микроорганизмами — лекарственные средства, оказывающие воздействие на них.
Предположим,
что в записи, связанной с узлом ОРГАНИЗМ-1 в этой структуре, хранятся данные
ГРАН = (ГРАМ-ОТР
1.0)
МОРФ = (ПАЛОЧКА
.8) (КОКОН .2)
ВОЗДУХ = (АЭРОБ
.6),
которые имеют
следующий смысл:
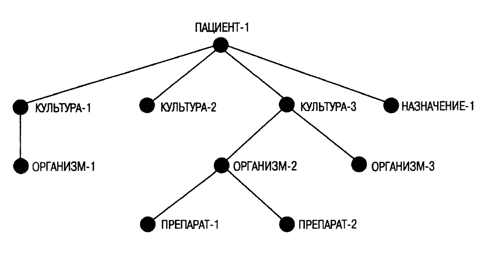
Рис. 3.3.
Типичное контекстное дерево в системе MYCIN ([Buchanan and Shortliffe, 1984])
Теперь предположим,
что применяется сформулированное выше правило. Нам требуется определить степень
уверенности в выполнении всех трех перечисленных в нем условий применительно
к данным, представленным в ОРГАНИЗМ-1. Степень уверенности в выполнении первого
условия равна 1.0, второго — 0.8, а третьего — 0.6. Степень уверенности в выполнении
совокупности условий принимается равной минимальному из значений, характеризирующих
отдельные компоненты, т.е. 0.6.
В качестве
оценки достоверности совокупности принимается минимальное значение по той причине,
что рассчитывать на выполнение всех условий вместе можно не более, чем на выполнение
самого "ненадежного" из них. Здесь очень уместна аналогия с цепочкой,
прочность которой не может быть выше прочности самого слабого ее звена. Можно
рассмотреть и обратный случай: какова степень уверенности в невыполнении
совокупности условий? Она равна максимальному из значений, характеризующих
невыполнение отдельных компонентов. Сформулированные выше соглашения легли в
основу методики формирования неточных суждений, так называемой нечеткой логики,
о которой мы поговорим в главе 9.
В данном
случае мы приходим к заключению, что микроорганизм, описанный в узле ОРГАНИЗМ-1,
относится к классу энтеробактерий со степенью уверенности, равной 0.6 х 0.8
= 0.48. Сомножитель 0.6 — это степень уверенности в выполнении совокупности
условий, перечисленных в правиле, а 0.8 — степень уверенности в том, что правило
дает правильное заключение, когда все означенные в нем условия гарантированно
удовлетворяются. За сомножителями и результатом этого выражения закрепился термин
коэффициента уверенности (CF— certainty factor). Таким образом,
в общем случае имеем:
СF(действие)
= СF(предпосылка) х СРF(правило)
Более подробно
о коэффициентах уверенности мы поговорим в главах 9 и 21, где основное внимание
уделяется теме представления неопределенности. Коэффициенты уверенности имеют
много общего с оценками вероятности, но между этими двумя понятиями есть и определенные
различия. Свойства этих коэффициентов не всегда подчиняются правилам теории
вероятности и, таким образом, с математической точки зрения вероятностями не
являются. Но методы вычисления коэффициентов уверенности некоторой совокупности
правил или действий по коэффициентам уверенности, характеризующим отдельные
компоненты в этой совокупности, в значительной мере напоминают методы вычисления
вероятности сложных событий по вероятностям совершения событий-компонентов.
3.3.3.
Структуры управления в MYCIN
Целевое правило
самого верхнего уровня в системе MYCIN можно сформулировать примерно так:
ЕСЛИ 1) существует
микроорганизм, который требует проведения курса терапии, и 2) заданы соображения
относительно любых других микроорганизмов, которые требуют проведения курса
терапии,
ТО сформировать
список возможных курсов терапии и выделить наилучший из них. В ходе консультации
выполняется простая двухэтапная процедура:
Применение
правила включает в себя оценку сформулированных в нем предпосылок, а этот процесс,
в свою очередь, включает проверку, существует ли микроорганизм, который требует
проведения курса терапии. Для этого сначала нужно выяснить, существует ли вообще
факт заражения микроорганизмами, связанными с определенными болезнями. Эту информацию
можно получить либо непосредственно от пользователя, либо воспользовавшись цепочкой
рассуждений, основанных на наблюдаемых симптомах и имеющихся данные лабораторных
исследований.
Консультация
представляет собой, по сути, поиск на древовидном графе целей. В корне дерева
располагается цель самого верхнего уровня — та часть целевого правила, в которой
отображено действие, — рекомендуемый курс лекарственной терапии. На более низких
уровнях размещаются подцели, которые представляют собой, например, выяснение,
какие микроорганизмы обнаружены в зараженных тканях и насколько заражение каждым
из них существенно. Многие из этих подцелей распадаются на более мелкие подцели.
Листьями дерева являются факты, которые не нуждаются в логическом выводе, поскольку
получены эмпирическим путем, например факты, установленные в лаборатории.
Для работы
программы очень удобно представить процесс порождения подцелей с помощью особого
вида структуры, названной И/ИЛИ-графом. Основная идея состоит в том,
что корневой узел дерева представляет главную цель, а терминальные узлы — примитивные
операции, которые может выполнить программа. Нетерминальные (промежуточные)
узлы представляют подцели, по отношению к которым допустимо выполнить дальнейший
анализ. Существует довольно простое соответствие между анализом таких структур
и анализом множества правил.
Рассмотрим
следующий набор правил "условие-действие":
Если
X имеет СЛУЖЕБНОЕ
УДОСТОВЕРЕНИЕ И
X имеет ОГНЕСТРЕЛЬНОЕ_ОРУЖИЕ,
ТО X - ПОЛИСМЕН.
ЕСЛИ
X имеет РЕВОЛЬВЕР,
или
X имеет ПИСТОЛЕТ,
или
X имеет ВИНТОВКУ,
ТО X имеет ОГНЕСТРЕЛЬНОЕ ОРУЖИЕ.
Если
X имеет ЛИЧНЫЙ_ЖЕТОН,
то
X имеет СЛУЖЕБНОЕ_УДОСТОВЕРЕНИЕ.
Эти правила
можно представить в виде набора узлов в дереве целей (рис. 3.4), в котором отражены
цели, которые выступают в совокупности, и те, которые воспринимаются независимо,
по одиночке. Между связями, идущими от узла ПОЛИСМЕН (корневой узел — главная
цель) к узлам СЛУЖЕБНОЕ_УДОСТОВЕРЕНИЕ и ОГНЕСТРЕЛЬНОЕ_ОРУЖИЕ, проведена дуга,
которая подчеркивает, что для удовлетворения главной цели необходимо удовлетворить
обе подцели. Но между связями, проведенными от узла ОГНЕСТРЕЛЬНОЕ_ОРУЖИЕ к узлам
РЕВОЛЬВЕР, ПИСТОЛЕТ и ВИНТОВКА, такой дуги нет, поскольку для удовлетворения
цели ОГНЕСТРЕЛЬНОЕ_ОРУЖИЕ достаточно удовлетворить любую из присоединенных подцелей.
Узел может иметь и единственного наследника, как узел СЛУЖЕБНОЕ_ УДОСТОВЕРЕНИЕ
на этом графе.
И/ИЛИ-граф
на рис. 3.4 можно рассматривать как способ представления пространства поиска
для цели ПОЛИСМЕН, перечислив все способы, которыми можно применить различные
операторы, чтобы достичь главной цели.
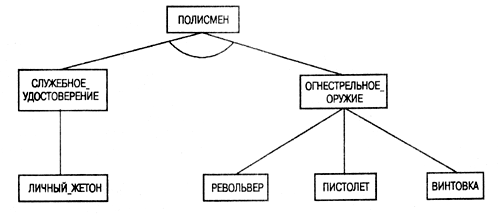
Рис. 3.4.
Представление набора правил в виде И/ИЛИ-графа
Такой вид
структуры управления правилами получил наименование цепочки обратного вывода
(backward chaining), поскольку путь рассуждений идет от того, что нужно
доказать, к фактам, на которых основывается доказательство. При прямой цепочке
рассуждение ведется, отталкиваясь от имеющихся фактов. В этом отношении система
MYCIN напоминает STRIPS, где цель также достигалась разбиением ее на подцели,
к которым можно было бы применить определенные операторы. Поиск решения в процессе
построения цепочки обратного вывода более целенаправлен, поскольку рассматриваются
только факты, потенциально способные повлиять на решение.
Структура
управления правилами в MYCIN использует И/ИЛИ-граф и по сравнению с программами
искусственного интеллекта довольно проста — в ней, по сути, использована методика
исчерпывающего поиска, описанная в главе 2, в которую внесены только незначительные
изменения.
(1) Формулировка
каждой подцели всегда представляет собой обобщенную форму исходной цели. Так,
если подцель состоит в том, чтобы доказать справедливость суждения "организм—
это E.Coli", то формулировка такой подцели— определение типа организма.
Этим инициируется исчерпывающий поиск, в который вовлекаются все возможные сведения
об организмах.
(2) В множестве
правил, подходящих для сформулированной цели, выискивается такое, которое определенно
удовлетворяется. Если для заключения об определенном параметре, например о природе
организма, подходит несколько правил, то их результаты объединяются (см. врезку
3.2). Если коэффициент уверенности какой-либо из выдвинутых гипотез оказывается
в диапазоне от -0.2 до +0.2, то гипотеза отбрасывается.
(3) Если
текущая подцель представляет собой лист на графе (терминальный узел), то данные
запрашиваются у пользователя. В противном случае устанавливается очередная подцель
и выполняется переход на шаг (1).
По завершении
процесса диагностики выбирается рекомендуемый курс лечения. Выбор включает две
стадии: отбор рекомендуемых медикаментов и предпочтительного варианта или комбинации
медикаментов из полученного списка.
3.2. Комбинация
гипотез
В системе
MYC1N может оказаться, что для суждения об определенном параметре подойдет не
одно правило, а несколько. Применение каждого из них — отдельная гипотеза —
характеризуется некоторым значением коэффициента уверенности. Например, из одного
правила следует, что данный микроорганизм— это E.Coli, причем коэффициент уверенности
этой гипотезы равен 0.8. Другое правило, принимая во внимание другие свойства
анализируемого объекта, приводит к заключению/что этот микроорганизм — E.Coli,
но эта гипотеза характеризуется коэффициентом уверенности 0.5 (или, например,
-0.8). Отрицательное значение коэффициента уверенности указывает, что данное
правило опровергает сформулированное заключение.
Пусть
х и у— коэффициенты уверенности одинаковых заключений, полученные при применении
разных правил. В таком случае в системе MYCIN используется следующая формула
определения результирующего коэффициента уверенности:
| { | X+Y-XY | при X,Y>0 | |
| CF(X,Y)= | { | X+Y+XY | при X,Y<0 |
| { | (X+Y)/(1-min(|X|,|Y|)) | при (X>0 и Y<0) или (X<0 и Y>0) |
Здесь
|Х| означает абсолютное значение X.
Что при
этом происходит, нетрудно понять интуитивно. Если обе гипотезы подтверждают
вывод (или, наоборот, обе гипотезы его опровергают), то коэффициент уверенности
их комбинации возрастает по абсолютной величине. Если же одна гипотеза подтверждает
вывод, а другая его опровергает, то наличие знаменателя в соответствующем выражении
сглаживает этот эффект.
Если оказалось,
что гипотез несколько, то их можно по очереди "пропускать" через эту
формулу, причем, поскольку она обладает свойством коммутативности, порядок,
в котором обрабатываются гипотезы, значения не имеет.
Отдельное
правило применяется по отношению к главной цели, представленной корневым узлом
на И/ИЛИ-графе. Если удовлетворяются все, связанные с ним предпосылки, то это
правило, вместо того чтобы формировать суждение, возбуждает определенное действие.
Здесь в системе MYCIN на сцену выходят правила формулировки рекомендаций о курсе
лечения. Эти правила включают информацию о чувствительности различных организмов,
известных системе, к тем или иным медикаментам. Ниже приведено простое правило
выдачи рекомендаций о лечении.
ЕСЛИ микроорганизм
идентифицирован как pseudomonas,
ТО рекомендуется
выбрать следующие медикаменты:
1 - COLISTIN
(0.98)
2 - POLYMIXIN
(0.96)
3 - GENTAMICIN
(0.96)
4 - CARBENICILLIN
(0.65)
5 - SULFISOXAZOLE
(0.64)
Числа, следующие
за названием каждого из перечисленных медикаментов, представляют оценки вероятности
Того, что бактерия pseudomonas окажется чувствительной к этому препарату,
и вводятся в систему исходя из существующей медицинской статистики. Предпочтительный
препарат из этого перечня выбирается с учетом противопоказаний, специфичных
для каждого пациента. Пользователь может пойти дальше и задавать вопросы об
альтернативном курсе лечения до тех пор, пока система не исчерпает список вероятных
диагнозов.
3.4.
Оценка и сравнение характеристик экспертных систем
Существует
множество способов оценки или сравнения характеристик экспертных систем, но
наиболее распространенный — сравнение полученных с их помощью результатов с
теми, которые получает человек-эксперт. При разработке системы инженер по знаниям
и эксперт работают вместе, добиваясь того, чтобы с помощью системы решить весь
набор типовых тестовых примеров. Затем системе предлагается решить "неизвестную"
ей проблему и анализируется, насколько полученный результат согласуется с полученным
экспертом.
Еще в 1974
году, на самой ранней стадии разработки системы MYCIN, были получены весьма
обнадеживающие результаты. Команда из пяти высококвалифицированных экспертов
в области диагностики инфекционных заболеваний подтвердила правильность 72%
рекомендаций, сделанных системой, которые относились к 15 реальным заболеваниям.
Главной проблемой оказалась не точность диагноза, а отсутствие правил, которые
позволяли бы судить о серьезности заболевания.
В 1979 году
были организованы более формальные испытания усовершенствованной версии MYCIN
по диагностике таких заболеваний, как бактеремия и менингит. Окончательное заключение,
вынесенное программой в 10 реальных случаях, сравнивалось с заключениями ведущих
медиков Станфордского университета и рядовых врачей, причем рассматривались
и такие случаи, в которых лечение уже проводилось. Затем были привлечены восемь
других экспертов, которых попросили оценить рейтинг 10 рекомендаций о курсе
лечения в каждом из рассмотренных случаев. Для каждого из предлагавшихся наборов
рекомендаций была определена максимальная оценка 80 баллов, причем экспертам
было неизвестно, что некоторые из них предложены не врачом, а компьютером. Результаты
представлены ниже.
|
Рейтинг по заключению
8 экспертов на основании 10 клинических случаев |
|||||
|
Максимально
возможная оценка — 80 баллов |
|||||
|
MYCIN |
52 |
Курс лечения,
назначенный в действительности |
46 |
||
|
Faculty-1 |
50 |
Faculty-4 |
44 |
||
|
Faculty-2 |
48 |
Resident |
36 |
||
|
Inf dis fellow |
48 |
Faculty-5 |
34 |
||
|
Faculty-3 |
46 |
Student |
24 |
||
|
Неприемлемый
курс лечения |
0 |
|
|
||
|
Одинаковые курсы
лечения |
1 |
|
|
||
Отличие между
оценкой, полученной MYCIN, и оценками качества рекомендаций ведущих специалистов
Станфорда, невелико, а по сравнению с рядовыми врачами система оказалась даже
на более высоком уровне.
Однако по
ряду причин (в том числе и перечисленных ниже) экспертная система MYCIN так
никогда и не использовалась в реальной врачебной практике.
Система MYCIN
при всей ее практической направленности была и осталась все-таки экспериментальной
исследовательской системой, не рассчитанной на коммерческое применение. Тем
не менее на ее основе были созданы другие экспертные диагностические системы,
которые реально использовались в лечебной практике (об одной из них — системе
PUFF — читайте в главе 13).
В этой книге
мы часто будем сталкиваться с оценкой качества отдельных моделей экспертных
систем, и вы увидите, что выработать какой-то общий подход к такой оценке, не
принимая во внимание специфику области применения, не удается. Однако можно
выделить ряд предварительных условий, которые необходимо соблюдать для адекватной
оценки качества экспертной системы любого назначения (этот вопрос обсуждается
в сборнике под редакцией Хейеса-Рота [Hayes-Roth et al, 1983, Chapter 8]).
Читателю
также должно быть ясно, что роль разных экспертных систем в той или иной предметной
области может быть совершенно различной, соответственно различными должны быть
и требования к ее производительности. Многие экспертные системы выполняют роль
советчика и предоставляют пользователю набор возможных вариантов решения проблемы.
В таком случае от системы требуется в основном сформировать как можно более
"емкий" перечень вариантов решения проблемы при заданных ограничениях,
причем система должна уложиться в разумное время. Другие системы предназначены
для формирования законченного решения проблемы, которое пользователь может принять
или отвергнуть. Учитывая, что последнее слово все-таки остается не за компьютером,
а за человеком, система может быть признана вполне работоспособной и в том случае,
если не все 100% предлагаемых ею решений правильны, но она должна быть способна
достаточно живо реагировать на запросы.
3.4.2.
Сравнение MYCIN и STRIPS
Возвращаясь
вновь к системе STRIPS, отметим, что, как показывает опыт работы с этой программой,
она способна решать только самые простенькие проблемы. Сложности появляются
при самых разных обстоятельствах. Вот только два примера.
Отчетливо
видно, что модель мира в системе STRIPS оказалась "бедной на знания",
т.е. она содержит очень мало специфических знаний о помещениях и объектах, которые
должны перетаскивать роботы, например о весе и габаритах объектов и размерах
дверных проемов в стенах. Для перемещения объектов используются только те эвристики,
которые содержатся в таблице операторов. Например, отсутствуют эвристики, позволяющие
избежать маршрутов движения через слишком узкие проемы, комбинировать перемещаемые
объекты с учетом грузоподъемности робота. Отсутствует также подготовительная
фаза, на которой можно было бы сгруппировать объекты, перемещаемые по близким
маршрутам.
Более широкие
возможности системы MYCIN в решении проблем проистекают от двух факторов: большой
набор правил, которые используются для формирования гипотез и способов подтверждения
их истинности, и большая база данных, в которой хранится информация о микроорганизмах,
медикаментах и лабораторных тестах. В то же время механизм управления применением
правил в MYCIN несколько проще, чем в STRIPTS. Основное различие между двумя
программами состоит не в отличиях между областями применения, а в способности
использовать декларативные знания в своей области.
В главе 2
мы обращали ваше внимание на то, что пионеры в области экспертных систем очень
быстро пришли к выводу, что лучше передать программе фактические сведения о
специфике предметной области и правила разного уровня абстракции, а затем применять
довольно простые правила влияния, чем передать системе информацию о более общих
законах, действующих в этой предметной области, и обобщенные алгоритмы целенаправленного
логического вывода. Человек-эксперт предпочитает действовать исходя из общих
законов только в особо трудных, необычных ситуациях, а в большинстве других
использует уже апробированные, знакомые ему решения.
Мы также
отметили, что одна из особенностей экспертных систем, отличающих их от обычных
программ, состоит в широком использовании эвристик, которые помогают минимизировать
количество шагов поиска при решении проблемы. Такой ускоренный путь решения
проблем воспроизводит и механизм мышления человека-эксперта, который применяет
базовые принципы только в редких случаях, а в большинстве ситуаций вполне удовлетворяется
решениями из накопленного опыта. В результате цепочка рассуждений оказывается
довольно короткой и крайне специфичной для каждой конкретной ситуации.
Использование
эвристик также означает, что процесс рассуждений в экспертной системе не всегда
может быть "озвучен", т.е. не всегда образует цепочку логической дедукции.
Инженер по знаниям должен не только решить, как структурировать знания
в базе знаний экспертной системы, но и как использовать эти знания в
процессе построения заключения. Структура машины логического вывода обычно определяется
как используемым представлением знаний, так и механизмом применения этих знаний.
Например, на любой стадии решения проблемы может сложиться ситуация, когда возможно
применение более чем одного правила (элемента знаний). Более того, эти правила
могут взаимно не согласовываться или даже быть противоречивыми. Так, в систему
планирования маршрута разносчика посылок могут быть заложены эвристические правила,
одно из которых гласит:
"Первыми
разнести посылки тем адресатам, которые расположены наиболее близко",
а второе:
"Избегать
выезда в предместья во время напряженного трафика".
Если окажется,
что довольно много адресатов компактно расположены в предместье, а расписание
разноски составлено так, что посылки нужно доставить как раз тогда, когда на
дорогах массовое движение, то эти два правила противоречат друг другу. Машина
логического вывода должна быть спроектирована так, чтобы справляться с подобными
противоречиями.
Довольно
распространено мнение, что способ, основанный на эвристиках, может привести
к ошибочному заключению, да и сами эвристики зачастую противоречивы. Тем не
менее эвристики широко используются в экспертных системах, поскольку во многих
областях их применения просто не существует надежных алгоритмов общего вида
для поиска решения, либо такие алгоритмы требуют огромных вычислительных ресурсов
в виду комбинаторного взрыва, т.е. экспоненциального роста сложности поиска
при линейном росте размерности задачи (об этом мы говорили в главе 2). Отсюда
ясно, почему при построении экспертных систем такое большое внимание уделяется
средствам представления узкоспециальных знаний в конкретной предметной области,
большинство из которых являются эвристиками. Подробный анализ различных схем
представления таких знаний будет проведен в главах 4-8.
Идеи планирования
операций, положенные в основу функционирования системы STRIPS, рассматриваются
во множестве книг, посвященных проблематике искусственного интеллекта (например,
[Givan and Dean, 1997]). Однако за время, прошедшее после появления STRIPS,
многие пришли к выводу, что использованные в ней методы требуют слишком больших
вычислительных ресурсов. В общем случае задача сводится к полному Р-пространству
[Bylander, 1994]. Нильсон предложил программную реализацию формализма
STRIPS [Nilsson, 1980], с версиями которой можно познакомиться на различных
университетских Web-страницах, например по адресу http: / /www. cs. brown. edu/research/ai.
Наиболее
полное описание системы MYCIN читатель найдет в работе [Shortliffe, 1976].
Анализ функциональных возможностей MYCIN и описание отдельных подсистем
содержится в работах [Buchanan and Shortliffe, 1984] и [Clancey and
Shortliffe, 1984]. В последней читатель найдет также описание некоторых
других ранних экспертных систем, ориентированных на медицинскую диагностику.
В работе [Cendrowska and Bramer, 1984] описана модификацию системы MYCIN
и приведено много интересных деталей реализации программы.
1. Что такое
таблица операторов? Можно ли в таблице операторов представить любую операцию,
выполнение которой хотелось бы потребовать от робота?
2. Что такое
порождающее правило? Какое, на ваш взгляд, существует соответствие между набором
порождающих правил и деревом решений?
3. Какая
связь существует между таблицами операторов и набором порождающих правил? Эквивалентны
ли они? Можно ли выразить одни в терминах других?
4. Представьте
себе, что манипуляционный робот смонтирован над столиком с детскими игрушками.
В таблице операторов имеется оператор move (В, L, М), который заставляет робот
перенести блок В из положения L в положение М.
move (В, L, M)
Предварительные условия on (В, L), clear (В), clear (M)
Список удалений on (В, L), clear (M)
Список
добавлений on
(В, L), clear (L), clear (столик)
Здесь выражение
on (В, L) означает, что блок В устанавливается на объект L, причем в качестве
L может выступать или поверхность столика, или другой блок; непосредственно
на один блок можно поставить только еще один блок, но на поверхность столика
можно ставить сколько угодно блоков; выражение clear (L) означает, что на объекте
L ничего не стоит.
I) Выразите
сцену, представленную на рис. 3.5, в виде формул модели мира.
II) Пусть
перед роботом поставлена цель перестроить башню, показанную на рис. 3.5, установив
блоки в следующем порядке: синий— на красном, красный — на зеленом, а зеленый
— на поверхности столика. Таким образом, перед роботом стоит цель преобразовать
модель мира и привести ее к виду
on(зеленый,
стол), on(красный, зеленый), on(синий, красный). Представьте план достижения
этой цели.
III) Покажите,
как будет изменяться база данных при выполнении плана в соответствии с таблицей
операторов.
IV) Почему
после каждой операции move нужно добавлять формулу clear (столик)?
V) Можно
ли, используя представленный элемент move в таблице операторов, выразить "отрицательную"
цель, например "зеленый блок не должен стоять
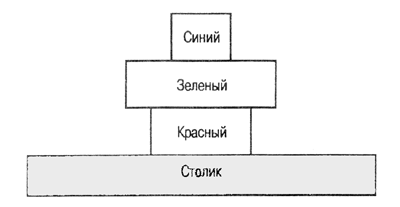
Рис. 3.5.
Задача о перемещении блоков
5. Как можно
удостовериться в правильности простого плана (как созданный в предыдущем примере),
в том смысле, что он гарантирует успешное достижение поставленной цели, предполагая,
что робот выполняет все операции правильно.
6. Можете
ли вы представить вид плана, который не может быть сформирован с помощью простого
формализма таблицы операторов, наподобие представленного в предыдущем упражнении.
7. Рассмотрим
правило системы MYCIN, представленное ниже:
ЕСЛИ
1) организм
обладает грамположительной окраской, и
2) организм
имеет форму колбочки, и
3) организм
в процессе роста образует цепочки,
ТО есть основания
предполагать (0,7), что этот микроорганизм относится к классу streptococcus.
Предположим,
что сформулированные в правиле условия характеризуются следующими коэффициентами
уверенности:
Условие 1:
0.8 Условие 2: 0.2 Условие 3: 0.5
Какой коэффициент
уверенности характеризует заключение о том, что данный организм относится к
классу streptococcus, которое вынесет MYCIN в соответствии со сформулированным
правилом?
8. Рассмотрим
такую пару правил системы MYCIN:
ЕСЛИ
1) культура
взята из анализа крови и
2) пациент
страдает повреждением кожи ecthyma gangrenosum,
ТО есть основания
предполагать (0,6), что этот микроорганизм относится к классу pseudomonas.
ЕСЛИ
1) тип инфекции
бактериальный и
2) пациент
имеет серьезные ожоги,
ТО есть слабые
основания предполагать (0,4), что этот микроорганизм
относится к классу pseudomonas.
Предположим,
что сформулированные в первом правиле условия характеризуются коэффициентами
уверенности 0.8 и 0.9, а сформулированные во втором правиле — коэффициентами
уверенности 0.2 и 0.3. Какой коэффициент уверенности будет характеризовать вывод,
что исследуемый микроорганизм относится к классу pseudomonas?
9. Начертите
И/ИЛИ-граф по типу приведенного в разделе 3.3.3 для следующего набора правил.
Если
ТОПЛИВО,
и
ВЫДЕЛЕНИЕ_ТЕПЛА,
и КИСЛОРОД,
то ПОЖАР
Если
ЖИДКОСТЬ и
ВОСПЛАМЕНЯЕМАЯ, то ТОПЛИВО
Если
ТВЕРДОЕ и
ГОРЮЧЕЕ, то ТОПЛИВО
Если
ГАЗ и
ГОРЮЧЕЕ, то ТОПЛИВО
Если
ПЛАМЯ и
ОТКРЫТОЕ, то ВЫДЕЛЕНИЕ_ТЕПЛА
Если
ЭЛЕКТРИЧЕСТВО,
ТО ВЫДЕЛЕНИЕ_ТЕПЛА
Если
ТРЕНИЕ,
ТО. ВЫДЕЛЕНИЕJTEIU1A. 10.
Выразите правила предыдущего упражнения средствами языка CLIPS (см. Приложение).