ГЛАВА
2.
Обзор
исследований в области искусственного интеллекта
В этой
главе...
Что такое
искусственный интеллект? Барр и Файгенбаум предложили следующее определение,
которое никем не оспаривается почти два десятка лет [Barr and Feigenbaum,
1981].
"Искусственный
интеллект (ИИ) — это область информатики, которая занимается разработкой интеллектуальных
компьютерных систем, т.е. систем, обладающих возможностями, которые мы традиционно
связываем с человеческим разумом, — понимание языка, обучение, способность рассуждать,
решать проблемы и т.д."
Другими словами,
исследования в области искусственного интеллекта направлены на разработку программ,
решающих такие задачи, с которыми сейчас лучше справляется человек, поскольку
они требуют вовлечения таких функций человеческого мозга, как способность к
обучению на основе восприятия, особой организации памяти и способности делать
выводы на основе суждений [Minsky, 1968].
Таким образом,
разработка программы, которая будет выполнять сложную статистическую обработку
данных, нельзя рассматривать как исследование в области искусственного интеллекта,
какие бы сложные алгоритмы в ней не использовались. А вот создание программы
порождения и проверки гипотез относится именно к этой области. Большинство людей
не обладают возможностью выполнять в уме арифметические действия уже с трехразрядными
числами, а компьютеры превосходно справляются с гораздо более сложными вычислениями.
Но, с другой стороны, разделить процесс проверки гипотез на
отдельные
эксперименты — это искусство, которое исследователь постигает как в результате
специального обучения, так и на собственном опыте. Составить компьютерную программу,
которая выполняла бы то же самое, — задача далеко не тривиальная.
Конечно,
как в каждой новой области, и здесь существуют разные точки зрения на главное
предназначение исследований по искусственному интеллекту. Некоторые ученые склоняются
к тому, что искусственный интеллект является ответвлением технических наук,
поскольку основное направление исследований в этой сфере — создание интеллектуальных
искусственных существ, скажем роботов [Nilsson, 1971]. Другие делают
упор на связях с теми областями, которые занимаются механизмом познания, — процессами
обработки информации в мозгу человека.
Но как бы
там ни было, никто не отрицает, что основные усилия в этой области предпринимаются
в направлении эмуляции мышления человека — разработке методов, которые позволили
бы запрограммировать машину таким образом, чтобы она могла моделировать (воспроизводить)
или даже превосходить способности человеческого разума. Исследования в этой
области тесно связаны со смежными — информатикой (наукой об обработке информации
с помощью компьютеров), психологией и лингвистикой. Тот факт, что исследования
в области искусственного интеллекта часто "вторгаются" в смежные области,
иногда приводит к определенным трениям в научной среде, но гораздо чаще результатом
является появление новых и неожиданных идей.
В этой главе
я постараюсь сделать краткий обзор исследований в области искусственного интеллекта,
выполненных за последние пять десятилетий, уделяя особое внимание тем из них,
которые имеют отношение к проблематике экспертных систем. Также будет рассмотрен
вопрос, в чем состоит отличие программирования, основанного на знаниях, от обычной
технологии программирования, с одной стороны, и обобщенных методов решения проблем,
которые развивали пионеры в области искусственного интеллекта, — с другой.
Историю исследований
в этой области, начиная примерно с 1950 года и по сегодняшний день, можно разделить
на три периода. За основу периодизации мы взяли те направления исследований,
которые наиболее активно развивались в течение каждого из них, — как в смысле
наибольшей активности ученых, так и в смысле получения наиболее существенных
практических результатов. Более подробную информацию о становлении искусственного
интеллекта как научного направления читатель найдет в книгах, перечисленных
в библиографической справке в конце главы.
2.1.
Классический период: игры и доказательство теорем
Исследования
в области искусственного интеллекта начались практически сразу же после появления
компьютеров и первых опытов по их применению для других, более "приземленных"
целей. Все началось с того, что вскоре после окончания Второй мировой войны
были предприняты попытки решать с помощью компьютера игровые задачи и головоломки.
Конечнтикой экспертных систем и недостаточно серьезны, чтобы дать что-нибудь
полезное для реальных приложений. Однако сейчас, оглядываясь назад, можно проследить,
как некоторые идеи и подходы к решению проблем с помощью компьютера выросли
именно из этих первых экспериментов.
2.1.1.
Поиск в пространстве состояний
Фундаментальная
идея, которая появилась в результате этих первых опытов, получила наименование
поиск в пространстве состояний. По существу, идея очень проста. Множество
проблем можно сформулировать в терминах трех важнейших ингредиентов:
Один из способов
представления такого концептуального пространства состояний — граф, в котором
состояниям соответствуют узлы, а операциям — дуги. Рассмотрим в качестве примера
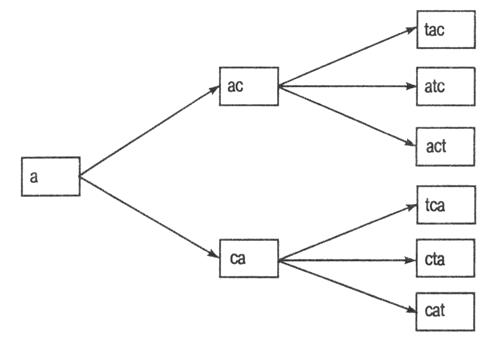
задачу построения слова из некоторого множества букв, как в игре Scrabble. Задавшись
набором операций установки букв, можно сформировать пространство состояний.
Предположим,
что множество доступных букв включает Т, С и А. На каждом уровне графа мы будем
добавлять по одной определенной букве. Каждая ветвь, исходящая из узла, соответствует
установке буквы в определенную позицию в последовательности, а эта последовательность
должна образовать осмысленное слово (рис. 2.1). Если это произошло, то головоломка
считается собранной (например, если образовалась комбинация "act"
или "cat"). (Сейчас мы не будем стремиться собрать какое-нибудь сложное
слово вроде "scrabble", которое может принести играющему больше очков.)

Рис. 2.1.
Дерево пространства состояний головоломки Scrabble с буквами Т, С и А
Это пространство
состояний обладает двумя интересными свойствами, которые присущи далеко не всем
пространствам состояний:
Метод формирования
анаграмм последовательным перечислением является примером применения алгоритма,
получившего наименование generate-and-test (порождение и проверка).
(1) Генерировать
новое состояние, модифицируя существующее; например, изменить последовательность
букв, добавив новую в существующую последовательность.
(2) Проверить,
не является ли образовавшееся состояние конечным (решением); например, проверить,
не является ли образовавшаяся последовательность осмысленным словом. Если это
так, то завершить, иначе перейти к шагу (1).
Множество
решений, которые удовлетворяют условию на шаге (2), иногда называют пространством
решений. В некоторых головоломках, например в уже упомянутой "8 ферзей",
решений много, а в других существует всего несколько или только одно. Действительно,
существует довольно много способов разместить восемь ферзей на шахматной доске
так, чтобы ни один из них не оказался под боем, а вот для головоломки "8-Puzzle"
существует единственное решение (см. упр. 7).
Алгоритм
имеет два основных варианта: поиск в глубину (depth-first search) и поиск
в ширину (breadth-first search). Отличаются варианты порядком формирования
состояний на шаге (1). Действительные алгоритмы приведены в упр. 5, а здесь
мы дадим только их неформальное описание.
Для любого
данного узла N алгоритм поиска в глубину строит потомок этого узла, т.е.
формирует состояние, которое образуется в результате применения операторов к
узлу N, а потом переходит к формированию узла, ближайшего к N, на
том же уровне графа ("соседу" N), т.е. формирует состояние,
которое образуется в результате применения оператора к узлу-родителю N. Алгоритм
поиска в ширину действует наоборот — сначала формируются все "соседи"
узла N, а потом уже строятся его потомки. Таким образом, в алгоритме
поиска в ширину просматриваются последовательно состояния, представленные узлами
одного и того же уровня на графе (рис. 2.2), а в алгоритме поиска в глубину
просматриваются состояния на одном пути, а затем происходит возврат назад на
один уровень и формируется следующий путь (рис. 2.3).
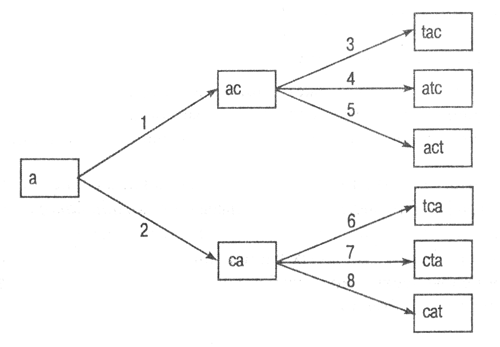
Рис. 2.2.
Граф пространства состояний при использовании алгоритма поиска в ширину
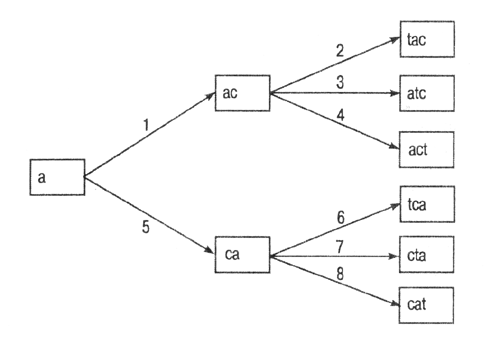
Рис. 2.3.
Граф пространства состояний при использовании алгоритма поиска в глубину
На обоих
рисунках числа на дугах графа указывают номер шага, на котором формируется тот
узел (состояние), для которого эта дуга является входящей. Конечно, этот номер
еще зависит и от того, в каком порядке используются операторы из имеющегося
множества. В представленном примере сначала применяется оператор, добавляющий
очередную букву в конец последовательности, затем оператор, добавляющий букву
на предпоследнюю позицию, и т.д., а последним применяется оператор, добавляющий
букву на первое место. Но ведь можно использовать и обратный порядок применения
операторов.
Оба алгоритма
завершат работу (найдут конечное состояние) после формирования узла "act",
а не "cat". Но алгоритму поиска в ширину придется для этого "посетить"
пять узлов (сформировать и проанализировать пять состояний), а алгоритму поиска
в глубину — четыре.
Отметим,
что свойства этих алгоритмов существенно отличаются.
Нетрудно
заметить, что число узлов растет экспоненциально по мере увеличения числа уровней
на графе. Это явление часто называют комбинаторным взрывом и оно представляет
очень серьезную проблему при программировании таких задач, например при "грубом"
переборе всех возможных вариантов позиций в игре в шахматы (см. врезку 2.1).
Поскольку человеческий мозг слабее компьютера при решении задач, связанных с
перебором вариантов, естественно предположить, что серьезный шахматист решает
эту задачу каким-то другим способом. Скорее всего он использует свой опыт, воображение
и аналитические способности, во-первых, для формирования общей стратегии игры,
а во-вторых, для выбора наилучшего очередного хода. Вот такой-то способ решения
мы и называем "интеллектуальным", в отличие от "грубого перебора".
В игровых
программах также используется поиск в пространстве состояний, но стратегия поиска
более избирательна, чем в случае прямого применения алгоритма generate-and-test.
Кроме того, нужно принимать во внимание и то, что в игре, как правило, принимают
участие две противоборствующие стороны. Были разработаны довольно неплохие программы
для игры в шашки, нарды и шахматы. Созданные программы игры в шахматы нельзя
отнести к классу систем, основанных на знаниях, а скорее к классу программ,
обладающих способностью избирательно анализировать пространство состояний, что
значительно повышает скорость и эффективность анализа. Методы и алгоритмы этого
класса в данной книге рассматриваться не будут.
Другая задача,
которая занимала умы исследователей в области искусственного интеллекта в середине
50-х годов, — доказательство теорем. Смысл задачи доказательства состоит
в том, чтобы показать, как некоторое утверждение, которое требуется доказать
(теорема), логически следует из декларированного множества других утверждений
или аксиом (которые полагаются истинными или являются такими
априори).
2.1. Комбинаторный
взрыв
Исследованием
вычислительной обозримости (или необозримости) проблем занимается
теория сложности. Для начала нам потребуется только знать, что существуют
классы проблем, решение которых требует ресурсов, экспоненциально возрастающих
при линейном увеличении размерности задачи. Например, время, необходимое
для отыскания пути в лабиринте, экспоненциально увеличивается при увеличении
количества разветвлений в лабиринте. Аналогично, время, необходимое для поиска
доказательства теоремы исчислением утверждений, растет экспоненциально по отношению
к количеству переменных. Такие проблемы являются в общем случае необозримыми
и называются NP-hard. Читателей, которые ими заинтересуются, мы отсылаем
к специальной литературе, в частности книге Хопкрофта и Ульмана [Hopcroft
and Ullman, 1979].
Проблемы,
время решения которых связано с размерностью задачи полиномиальной функции,
считаются обозримыми. Например, проверка заданного маршрута в лабиринте или
проверка правильности доказательства некоторой теоремы — обозримые проблемы.
Но можно показать, что, к сожалению, большинство проблем, которые интересуют
нас в области искусственного интеллекта, относятся к классу NP-hard. Поэтому
такое важное значение придается использованию эвристических методов при их решении.
Прекрасное
изложение теории вычислительной сложности, рассчитанное на читателя, несклонного
к излишнему теоретизированию, можно найти в работе Паунд-стоуна [Poundstone,
1988, Chapter 9].
Рассмотрим
такой пример. Пусть имеются две аксиомы, представленные на некотором формальном
языке:
"Если
компьютер может ошибаться, он ошибется" и
"Мой
компьютер может ошибаться".
Тогда, используя
механизм исчислений только правил влияния, мы можем показать, что справедлива
теорема.
"Мой
компьютер ошибется".
Это утверждение
логически следует из заданных аксиом в том смысле, что оно не может быть ложным,
если истинны исходные утверждения (аксиомы). Корректности такого следствия легко
доказываются компьютером — все, что от него требуется, так это обработать выражения
в форме логической зависимости:
(любой Х)(F(X))
![]() G(X))
G(X))
F(a) / [G(a){X/a}]
которое читается
следующим образом:
"Все
элементы F являются элементами G, а входит в F, следовательно,
F есть G".
Как и в случае
с головоломками, некоторые концепции и методы, разработанные в области машинного
доказательства теорем (иногда эту область исследований называют automated
reasoning — машинным поиском логического вывода), весьма помогут
студентам при решении практических проблем. Итак, знания, касающиеся решения
некоторой проблемы, можно представить как набор аксиом, т.е. теорию, а
процесс поиска решения проблемы можно рассматривать как попытку доказать теорему,
каковой является искомое решение (подробнее об этом — в главе 8). Другими
словами, поиск решения среди сформулированных теорем аналогичен поиску пути
на графе в пространстве состояний и для его анализа можно использовать тот же
аппарат.
К сожалению,
процесс порождения всех возможных теорем, вытекающих из заданного множества
аксиом, имеет все черты комбинаторного взрыва, поскольку на основе первичных
теорем, непосредственно вытекающих из аксиом, можно сформулировать новое
множество теорем и т.д. Поиск решения посредством доказательства теорем может
повлечь за собой такое количество вычислений, с которым не справится никакой
мыслимый компьютер, и можно доказать, что некоторые из таких вычислений даже
теоретически никогда не смогут завершиться. В области машинного поиска логического
вывода существенные успехи достигнуты в направлении, которое связано с генерацией
формальных математических доказательств, но эти методы с трудом приложимы к
менее формализованным областям. Поскольку большинство человеческих особей не
обладают выдающимися способностями в области построения логических выводов,
да еще принимая во внимание комбинаторные сложности, вряд ли стоит рассчитывать
на существенное влияние участия человека в формальных рассуждениях такого рода.
Скорее помощь может проявиться в том, что человек сможет делать более правдоподобные
предположения или порождать более вероятные гипотезы, носящие неформальный характер.
Это именно тот вид заключений, который используется при моделировании путей
поиска решения реальных проблем в экспертных системах.
Поскольку
слепой поиск возможен только в небольшом пространстве вариантов, напрашивается
совершенно естественный вывод, что необходим некоторый способ направленного
поиска. Если такой способ использует при поиске пути на графе в пространстве
состояний некоторых знаний, специфических для конкретной предметной области,
его принято называть эвристическим поиском. Лучше всего рассматривать
эвристику в качестве некоторого правила влияния, которое, хотя и не гарантирует
успеха (как детерминированный алгоритм или процедура принятия решения), в большинстве
случаев оказывается весьма полезным.
Простая форма
эвристического поиска — это восхождение на гору. В процессе поиска в
программе использует некоторая оценочная функция, с помощью которой можно
грубо оценить, насколько "хорошим" (или "плохим") является
текущее состояние. Затем можно применить ту же функцию для выбора очередного
шага, переводящего систему в следующее состояние.
Например,
простая оценочная функция для программы игры в шахматы может включать очевидную
оценку материала (количества и качества имеющихся на доске фигур) — своего и
соперника. Затем программа перебирает возможные операторы перехода в новое состояние
(возможные ходы фигур) и, сравнивая результаты вариантов, отыскивает такой,
который характеризуется максимальным значением оценочной функции. Другими словами,
ищется такой ход, который дает наибольший материальный выигрыш.
Основной
алгоритм, реализующий идею восхождения на гору, можно сформулировать следующим
образом.
(1) Находясь
в данной точке пространства состояний, применить правила порождения нового множества
возможных решений, например множества ходов фигур, допустимых в данной позиции.
(2) Если
одно из новых состояний является решением проблемы, прекратить процесс. В противном
случае перейти в то состояние, которое характеризуется наивысшим значением оценочной
функции. Вернуться к шагу (1).
Но применение
этого подхода наталкивается на хорошо известные трудности. Главная из них —
как сформулировать оценочную функцию, которая адекватно бы отражала "качество"
текущего состояния. Продолжая наш пример с игрой в шахматы, заметим, что иметь
много фигур, больше чем у соперника, отнюдь не значит иметь лучшую позицию,
т.е. быть ближе к успеху. Такая простая оценочная функция не учитывает многих
особенностей этой игры (а в более широком контексте — особенностей данной предметной
области).
Более того,
даже если оценочная функция и позволяет адекватно оценить текущую ситуацию,
сущестЬуют разнообразные ситуации игры, которые сами по себе могут быть источником
затруднений. Например, в данном состоянии нет очевидного очередного хода, т.е.
оказывается, что все возможные ходы одинаково хороши (или плохи). Это не что
иное, как выход на "плато" в нашем восхождении, когда ни один из возможных
путей не влечет за собой подъем. Другой возможный источник затруднений — наличие
локальных максимумов, из которых возможен только спуск, т.е. "ухудшение"
состояния. Например, я могу взять вашего ферзя и после этого проиграть партию.
Лучшими свойствами
обладает другая форма эвристического поиска, которая получила наименование сначала
наилучший (best-first search). Так же, как и в варианте восхождения на
гору, в нашем распоряжении имеется оценочная функция, с помощью которой
можно сравнивать состояния в пространстве состояний. Основное же отличие нового
метода от ранее рассмотренного состоит в том, что сравниваются не только те
состояния, в которые возможен переход из текущего, но и все, до которых
"можно достать".
Такой алгоритм,
естественно, требует значительно больших вычислительных ресурсов, но идея состоит
в том, чтобы принимать во внимание не только ближайшие состояния, т.е. локальную
обстановку, а "окинуть взглядом" как можно больший участок пространства
состояний и быть готовым, в случае необходимости, вернуться туда, где мы уже
были, и пойти другим путем, если ближайшие претенденты не сулят существенного
прогресса в достижении цели (см. описание алгоритма А во врезке 2.2). Вот эта
возможность отказаться от части пройденного пути во имя глобальной цели и позволяет
найти более эффективный путь. Необходимость хранить ранее сделанные оценки состояний
и постоянно их обновлять, конечно, требует значительных вычислительных ресурсов.
2.2. Алгоритм
А
Существует
хорошо известный алгоритм поиска, который относится к группе первый лучший,
получивший наименование А (произносится "А со звездочкой"). Основная
идея алгоритма состоит в использовании для каждого узла п на графе пространства
состояний оценочной функции вида
f(n) =
g(п) + h(n).
Здесь g(п)
соответствует расстоянию на графе от узла п до начального состояния,
a h(n) —оценка расстояния от п до узла, представляющего конечное
(целевое) состояние. Чем меньше значение оценочной функции f(n), тем
"лучше", т.е. узел п лежит на более коротком пути от исходного
состояния к целевому. Идея алгоритма состоит в том, чтобы с помощью f(n)
отыскать кратчайший путь на графе от исходного состояния к целевому.
Отсюда следует,
что если h(n) — нижняя оценка действительного расстояния до целевого
состояния, т.е. если h(n) никогда не дает завышенной оценки расстояния,
то алгоритм А всегда отыщет оптимальный путь до цели при помощи оценочной функции
f(n). Алгоритм, обладающий таким свойством, называется разрешимым (более
подробное обсуждение этого вопроса читатель найдет в специальной литературе,
в частности в работах Нмпьсона [Nilsson, 1980, Chapter 2] и Перла [Pearl,
1984, Chapter 2]).
Обозначения:
s — узел
начального состояния;
g—
узел целевого состояния;
OPEN — список,
который содержит,выбранные, но необработанные узлы;
CLOSED —
список, который содержит обработанные узлы.
Алгоритм
(1) OPEN:={s}.
(2) Если
ОРЕМ:={}, то прекратить выполнение. Пути к целевому состоянию на графе не существует.
(3) Удалить
из списка OPEN узел п, для которого f(n)<f(m) для любого узла т,
уже присутствующего в списке OPEN, и перенести его в список CLOSED.
(4) Сформировать
список очередных узлов, в который возможен переход из узла n и удалить из него
все узлы, образующие петли; с каждым из оставшихся связать указатель на узел
п.
(5) Если
в сформированном списке очередных узлов присутствует д, то завершить
выполнение. Сформировать результат — путь, порожденный прослеживанием указателей
от узла д до узла s.
(6) В противном
случае для каждого очередного узла n', включенного в список, выполнить следующую
последовательность операций.
Если old<new,
прекратить обработку нового узла.
Если new<old,
заменить новым узлом прежний в списке, причем, если прежний узел
был в списке
CLOSED, перенести его в список OPEN.
Конец
алгоритма
Применение
этого алгоритма рассмотрено в упр. 8.
Вычислительная
мощность современных компьютеров все-таки недостаточна для того, чтобы использовать
алгоритмы поиска решений даже с помощью направленного поиска с применением оценочной
функции, не говоря уже о методике слепого перебора возможных состояний. Пространство
состояний, в котором нужно вести поиск, при решении таких задач, как распознавание
речи, выбор конфигурации компьютерной системы или планирование последовательности
операций, настолько велико, что его невозможно проанализировать такими обобщенными
методами за обозримый отрезок времени, если только не призвать на помощь знания,
касающиеся конкретной предметной области. Можно показать, что многие из этих
проблем изоморфны абстрактным задачам, которые заведомо относятся к классу "необозримых"
в том смысле, что их сложность, а соответственно и потребность в вычислительных
ресурсах, экспоненциально возрастает при линейном увеличении размерности задачи.
Как будет
показано далее, развитие экспертных систем пошло по пути привлечения опыта экспертов,
как касающегося деталей поведения конкретных объектов в конкретной ситуации,
так и стратегии логического вывода в определенной предметной области, что и
позволяет преодолеть трудности, связанные со сложностью формализованного поиска
в пространстве состояний.
Достаточно
подробно результаты первых исследований в области программирования игр и машинного
доказательства теорем описаны в сборнике статей под редакцией Фей-генбаума и
Фельдмана [Feigenbaum and Feldman, 1963]. Я склонен к тому, чтобы считать
"классическим" в истории искусственного интеллекта период, который
начался с публикации в 1950 году статьи Шеннона об игре в шахматы [Shannon,
1950] и закончился выходом сборника Фейгенбаума и Фельдмана. Наиболее существенные
результаты, полученные в этот период, можно сформулировать следующим образом:
Очень редко
удается свести использование знаний к формулировке адекватной оценочной функции
и таким образом помочь программе оценить свое поведение в текущей ситуации и
найти правильный путь к решению. Но в большинстве случаев требуется нечто большее,
что-то вроде глобальной стратегии решения проблем или явного использования знаний
об объектах, их свойствах и связанных с ними действиях в конкретной предметной
области, или комбинации того и другого.
2.2.
Романтический период: компьютер начинает понимать
Период от
середины 60-х до середины 70-х я называю "романтическим" в истории
исследований искусственного интеллекта. В это время внимание исследователей
сосредоточилось в основном на проблеме машинного "понимания", т.е.
способности воспринимать естественный язык человека, в частности вести осмысленный
диалог. Эти попытки были встречены философами с определенным скепсисом. Они
сомневались в том, что по отношению к компьютерной программе вообще можно употреблять
слово "понимание".
Кульминационным
моментом этой эпохи явилась разработка Виноградом [Winograd, 1972] системы
SHRDLU, которая понимала довольно представительное подмножество слов английского
языка и делала определенные выводы в ограниченной области (в мире, построенном
из деталей детского конструктора). Программа демонстрировала свои возможности
восприятия речевых команд, реконструируя созданный ею "мир деталей"
и отвечая на вопросы, касающиеся как конфигурации деталей, так и своих действий
с ними. Она могла отвечать на вопросы вроде следующих:
"Какого
цвета блок, на котором стоит красная пирамида?" и строить план выполнения
команды, например: "Поставь синюю пирамиду на зеленый кубик".
Можно было
считать, что система SHRDLU понимает фразы на человеческом языке, поскольку
она адекватно на них реагировала. "Разумность" такого рода восприятия
была названа "процедуральной семантикой". Вывод о разумности программы
основывался на идее, что если программа способна в ответ на вопрос выполнить
соответствующие действия, то можно считать, что она "поняла" заданный
вопрос. Такая точка зрения на проблему машинного "понимания" основывается
на воспроизведении в первую очередь поведенческой реакции, а не способностей
человеческого мышления.
Другое направление
исследований было связано с попытками воспроизвести механизм понимания в менее
искусственном и более близком к реальному контексте, например в ситуаиии
визита к врачу или посещения ресторана. Шанк и Колби [Schank and Colby, 1973]
воспользовались структурой, названной ими сценарием, для объединения разнообразных
элементов, представляющих в совокупности реальную ситуацию. Сценарий можно рассматривать
как объединение разнообразных целей, решений и обычаев, связанных с определенными
событиями. Так, "сценарий посещения ресторана" приводится в действие
при возникновении цели "чего бы съесть", удовлетворяется событием
"прием пищи" и объединяет промежуточные знания о том, как заказать
столик, выбрать блюда в меню, расплатиться, дать на чай и т.п. Такое объединение
целей и средств, характерных для определенной ситуации, объясняет, почему определенные
действия считаются нормой в одной ситуации и рассматриваются как неадекватные
в другой. Например, раздевание в присутствии постороннего является нормой при
визите к врачу и рассматривается как неадекватное при посещении ресторана. Такой
же подход позволяет включить и некоторые знания, которые мы считаем само собой
разумеющимися, — любой под визитом к врачу понимает посещение клиники, а не
квартиры врача. В сценарии "визит к врачу" это учитывается включением
в качестве места посещения по умолчанию именно клиники.
2.3. Сценарий
посещения ресторана
Для описания
сценария можно использовать разные системы обозначений, но все они должны содержать
определенные базовые компоненты: цель, которой должны удовлетворять все действия
в этом сценарии, предварительные условия, которые должны быть удовлетворены
перед тем, как сценарий можно будет применить, и заключительные условия, характеризующие
ситуацию после завершения применения сценария. В системе обозначений также должны
быть предусмотрены разделители между отдельными фазами сценария, которые служат
для организации некоторых действий. Ниже приведен простой сценарий визита в
ресторан.
Цель: поесть
без самостоятельного приготовления пищи. Предварительные условия: голоден, есть
деньги, ресторан работает. Состояние после завершения: сыт, денег стало меньше.
Действие
первое: войти в ресторан. Найти место самостоятельно, если нет никаких других
признаков, что на вас обратили внимание, или отсутствует метрдотель. В противном
случае позволить метрдотелю найти место.
Действие
второе: просмотреть меню, сделать заказ,и поесть. Не забыть, что в ресторане
могут быть фирменные блюда.
Действие
третье: получить чек. Заплатить официанту/официантке или кассиру. Покинуть заведение.
Обратите
внимание на то, что в разных ресторанах существуют отличительные способы выполнения
похожих действий, — по-разному отыскивается место за столиком, предлагаются
свои фирменные блюда, выполняется расчет за услуги. Такие нюансы также можно
зафиксировать в сценарии, что позволит сформировать поведение, адекватное конкретной
ситуации. В идеале, в сценарии могут быть зафиксированы разные варианты поведения,
в зависимости от выполнения тех или иных условий, специфицированных в компоненте
"Предварительные условия".
Применение
механизма сценариев можно рассматривать в свете проблемы представления знаний
на более высоком уровне, чем в случае процедуральной семантики. Описание понятия
на уровне отдельной фразы нельзя "поднять" на более высокий уровень,
когда нужно принимать во внимание эпизод в целом вместе с множеством мотиваций,
подразумеваемых, но никогда (или редко) не формулируемых человеком вслух. Некоторые
исследователи пришли к выводу, что зависимость от контекста является главным
препятствием в решении проблемы компьютерного понимания естественного языка.
В результате были начаты исследования в направлении, где предпочтение отдается
не формальным моделям языка и сопряженных с его восприятием мыслительных процессов,
независимых от конкретной предметной области, а относительно неформальным, контекстным
способам рассуждений.
Другие исследователи
(например, [Newell and Simon, 1972] и [Anderson, 1976]) попробовали
на несложных задачах (простенькие головоломки, игры в слова и тесты, оценивающие
способность к запоминанию) смоделировать присущий человеку подход к решению
проблем. Они стремились сделать так, чтобы знания и стратегия поведения программы
как можно больше походили на знания и стратегию поведения человека в аналогичной
ситуации. Оценка успешности моделирования производилась путем сравнения поведения
человека и программы при решении одной и той же задачи.
Но такое
компаративное изучение сталкивается с фундаментальной проблемой — не существует
прямого метода показать, что человек и программа искусственного интеллекта делают
одни и те же вещи одинаковым способом. В результате используется косвенная аргументация.
Например, демонстрируется, что человек и программа делают аналогичные ошибки,
если встречаются с проблемой повышенной сложности и ошибочными данными, или
что распределение времени на выполнение одинаковых этапов решения задачи у человека
и программы имеет одинаковый характер при решении аналогичных задач различных
классов. Общепринятой стала точка зрения, что простое совпадение ответов на
одинаковые вопросы — недостаточное доказательство совпадения способов рассуждений,
поскольку существует множество отличающихся стратегий и способов использования
имеющихся знаний, которые можно применить для решения одной и той же проблемы.
2.2.2.
Схемы представления знаний
Независимо
от того, насколько это вторжение в науку о познании было продуктивным для психологии,
оно способствовало весьма существенному прогрессу в информатике. Ньюэлл (Newell)
и Саймон (Simon) предложили схему, известную как набор порождающих правил
(production rules). (Подобно мы поговорим о ней в главе 5.) Со временем
порождающие правила стали основным инструментом при проектировании экспертных
системы. Ньюэллу и Саймону также принадлежит приоритет в разработке методики,
получившей наименование анализ протокола (protocol analysis). Эта методика
заключается в том, что человеку предлагается "думать вслух" в процессе
решения проблемы, а затем зафиксированный протокол анализируют и пытаются отыскать
в нем концепции и процедуры, которые были использованы человеком. Этот подход
можно считать предшественником используемой сегодня методики извлечения знаний.
Уже первые исследования на стыке психологии и информатики показали, насколько
сложной является проблема представления знаний, но они также и продемонстрировали,
что ее решения следует искать скорее на пути эмпирических исследований, чем
философских дебатов.
В романтический
период было предпринято множество исследований, целью которых было выяснить,
каким образом и многообразие сведений об отдельных фактах, и общие принципы
построения окружающего нас мира можно использовать в компьютерной программе,
которая ориентирована на построение логического рассуждения, направленного на
достижение определенной цели. Эти исследования включали использование конструкций
следующих видов (чаще в чистом виде, но иногда и в комбинации):
Следует отметить,
что большинство созданных в этот период программ носили только исследовательский
характер. Лишь немногие работы получили продолжение и воплотились в нечто, приложимое
к реальным задачам.
Весьма репрезентативная
подборка статей, написанных в первой половине этого периода, опубликована Минским
[Minsky, I968J. Любая из них представляет интерес, но далеко не все убедительны
с точки зрения достижений сегодняшнего дня. Тем не менее множество схем представления
знаний, которым мы отдаем предпочтение в современных разработках, основаны именно
на результатах, полученных в тот романтический период. Например, в работе Квилиана
(Quillian) предложены ассоциативные и семантические сети в качестве
графического формализма для описания фактов и определений (подробнее об этом—
в главе 6). Без результатов, полученных в это время, вряд ли разработчики современных
экспертных систем располагали бы таким разнообразием функций и структур.
Наиболее
интересные работы, опубликованные во второй половине этого периода, собраны
Уинстоном [Winston, 1976,b]. Среди них я настоятельно рекомендую ознакомиться
с фундаментальной работой Минского о формализме представления знаний, получившем
наименование фреймов. Работы, выполненные в этом направлении в 70-е годы
в Массачусетсском технологическом институте, собраны в двухтомнике Уинстона
и Брауна [Winston and Brown, 1979]. Здесь вы найдете множество статей
и о тех областях искусственного интеллекта, которые выходят за рамки этой книги,
в частности о машинном восприятии естественного человеческого языка, искусственном
зрении, робототехнике.
2.4. Летучие
мыши и проблема с пингвинами
Семантические
цепи представляют собой средство представления знаний, базирующееся на формализме
теории графов. В таксономическом графе на рис. 2.4 представлены наши познания
о птицах, перепончатокрылых млекопитающих и даже специфических видах рыб— летающих.
Однако птицы являются куда более типичными представителями летающих животных,
чем, скажем, летучие мыши (перепончатокрылые млекопитающие), которые, в свою
очередь, более распространены, чем летающие рыбы. Этот факт никак не отражается
на простом графе.
Аналогично,
простой граф "умалчивает" и о другом факте. Несмотря на то что подавляющее
большинство птиц способно летать, этого нельзя сказать о пингвинах. Как же отразить
на графе исключение из общего правила. Некоторые из возможных ответов вы найдете
в главе 6.
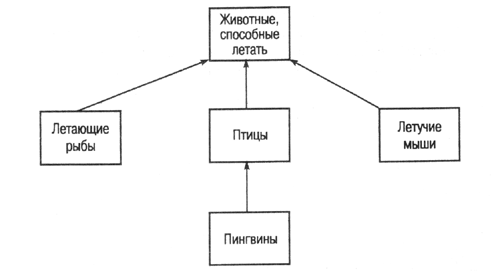
Рис. 2.4.
Простой таксономический граф, не учитывающий исключений
Конечно,
вряд ли исследования в области машинного "понимания" будут завершены.
Сейчас мы даже не знаем, при каких условиях можно сделать заключение, что машина
все понимает. Но если мы не можем со всей уверенностью четко сформулировать,
что представляет собой фундамент машинного понимания, можно, по крайней мере,
перечислить его необходимые составляющие.
Первая —
это способность представлять знания об окружающем мире и формулировать суждения,
основываясь на таких представлениях. В экспертных системах эта способность демонстрируется
на практике с учетом того, что в таких системах представляются знания о конкретной
предметной области, соответственно и порождаемые ими суждения относятся только
к этой области. Как и программа Винограда, экспертная система выглядит весьма
ограниченной в смысле объема знаний, а вероятность получить достоверное с нашей
точки зрения суждение обратна объему знаний, вовлеченных в вывод суждения.
Другим признаком
"понимающей" машины является способность находить эквивалентность
или аналогию между разными представлениями в одинаковых ситуациях. Здесь, конечно,
счет далеко не в пользу экспертных систем, поскольку в таких системах ввод информации
выполняется в совершенно определенной, жесткой форме, полностью соответствующей
запасенным в системе знаниям. Любое отклонение от ожидаемой схемы может привести
к практически непредсказуемым последствиям.
И последнее—
понимание предполагает способность обучаться каким-либо нетривиальным способом.
В частности, новая информация должна интегрироваться в уже имеющееся знание
и, возможно, модифицировать его. Такие способности редко демонстрируются в современных
экспертных системах, хотя в последние годы и наметился определенный прогресс
в области машинного обучения (подробнее об этом читайте в главе 20).
Нужно отметить,
что современные экспертные системы еще слабо соответствуют многим из этих критериев,
но вывод о том, что они не обладают "пониманием" хотя бы в отдельной
предметной области, также спорен. В своей области каждая из современных экспертных
систем "понимает", т.е. способна решать проблемы, ненамного хуже,
чем человек [Davis,
1989]. Ряд хорошо описанных систем решает свои задачи на таком же уровне,
что и человек-эксперт, хотя и не демонстрирует "понимания"
того вида, которым так были озабочены исследователи в описываемый романтический
период. Дэвис настаивает на том, что не существует связи на уровне необходимости
между частным процессом решения проблемы и самим решением. Другими словами,
все, что нам требуется от экспертной системы, — это получить ответ, более или
менее близкий к тому, который дает эксперт-человек, или помочь человеку дать
правильный ответ. Нам отнюдь не требуется, чтобы система в процессе получения
ответа повторяла ту же последовательность рассуждений, что и человек, или точно
таким же способом организовала свои знания о предметной области.
Однако в
главе 11 и далее мы увидим, что попытки использовать экспертную систему для
преподавания наталкивают на мысль о необходимости пересмотреть эту точку зрения.
Результаты последних исследований в области совершенствования экспертных систем
подталкивают нас все ближе к расплывчатым целям машинного "понимания".
Эти же результаты породили и новый взгляд на процесс решения проблем человеком
и предоставили в наше распоряжение значительно более широкий набор концепций,
пригодных для анализа активности как человека, так и машины при решении проблем.
2.3.
Период модернизма: технологии и приложения
Период, который
я называю периодом модернизма, продолжался с середины 70-х до конца 80-х годов.
Он характеризуется значительным прогрессом в области экспертных систем, так
называемой "зимней спячкой" в области "чистого" искусственного
интеллекта, интерес к которому возобновился с появлением Всемирной паутины.
То время, когда готовилось к печати настоящее издание, я отношу уже к следующему
периоду— периоду постмодернизма, от характеристики которого я здесь воздержусь,
поскольку сам являюсь участником происходящего в нем. Но, не боясь ошибиться,
можно утверждать, что происходящее в нем во многом определяется развитием Internet-приложений,
в частности интеллектуальных агентов и советчиков, облегчающих и упрощающих
извлечение информации при работе со средствами электронной коммерции. Успехи
и неудачи в области искусственного интеллекта в этот период в значительной мере
зависят от возможности и желания исследователей преодолеть влияние традиционных
концепций, характерных для прежних периодов, и сосредоточить усилия на реальных
проблемах новой информационной среды.
В период
модернизма возросла уверенность, что эвристические возможности "решателя"
проблем определяются представлением в явной форме соответствующих зданий, доступных
программе, а не применением какого-то изощренного механизма определения взаимовлияния
или сложных оценочных функций. Значительные усилия были направлены на разработку
методов разбиения знаний, присущих человеку, на модули, которые можно было бы
активизировать по заданной схеме (см. врезку 2.5). Уже при первых попытках сымитировать
процесс разрешения проблем, характерный для человеческого разума (например,
в работе [Newell and Simon, 1972]), исследователи столкнулись с ограниченными
возможностями представления знаний и необходимостью упростить механизм их взаимовлияний,
хотя более поздние исследования и помогли
в определенной степени преодолеть эти трудности (об этом мы поговорим в главах
11-18).
Стало ясно,
что стратегия явного представления человеческого знания в форме направляемых
заданной схемой модулей обладает определенными преимуществами перед включением
знаний в алгоритм, которые могут быть реализованы с помощью программных технологий,
более близких к традиционным.
В этот период
разработчики на практике убедились в том, как сложно создавать и отлаживать
системы, базирующиеся на правилах. По мере расширения базы знаний оказалось,
что правила имеют тенденцию взаимодействовать в пределах системы самым неожиданным
образом, соревнуясь за приоритет при решении проблемы, что разные режимы управления
правилами эффективны для проблем одного типа и не дают эффекта при решении проблем
другого типа. Со временем в этом перестали видеть что-то необычное, но поначалу
свидетельства такого эффекта воспринимались как анекдоты.
Практический
опыт научил нас, что наилучшие результаты при решении проблем разного рода можно
получить, только используя отличающиеся методики. Эти методики, получившие звучные
и исполненные тайного смысла наименования "эвристическая классификация",
"иерархическая проверка гипотез" и "предложение, проверка и исправление",
как правило, сводятся к разным стратегиям управления последовательностью применения
правил. Эти методики будут подробно рассмотрены в главах 11-15.
2.5. Процедуральное
или декларативное знание
В процедурных
языках программирования, таких как С, мы, как правило, физически не разграничиваем
ту часть программы, которая описывают ее "логику", от той, которая
имеет дело с манипулированием данными. Например, процедура, в которой проверяется,
обладает ли данная птица способностью летать, будет выглядеть так:
char fly(char
s)
{
char answer = 'д'; if (strcmpfs, "пингвин")==0)
{ answer = 'н';} return answer;
}
Независимо
от того, владеете вы языком С или нет, понятно, что этот программный код явно
вызывается другой частью программы, например, так:
char с;
с = fly("пингвин");
Предположим,
что вместо этого у нас есть два правила, которые хранятся в базе знаний:
(defrule
(птица (тип
?Х)) =>
(assert (да))
)
(defrule
(птица (тип
пингвин)) =>
(assert (нет))
)
В этом примере
форма правил более близка к объявлению или определению (использован- синтаксис
языка CLIPS). Для случайно выбранной птицы утверждается, что она способна летать.
Но если известно, что птица — это пингвин, то утверждается, что она не способна
летать. Но поскольку пингвин это тоже птица, то какой-то другой компонент экспертной
системы должен решить, какое из этих двух правил применять в данной ситуации.
Этот компонент называется машиной логического вывода (inference engine).
В этом
примере совершенно отчетливо видна модульная природа правил. Код, который в
явном виде вызывает то или иное правило, отсутствует. Подробно реализация
таких правил будет рассмотрена в главе 5.
В этот период
появился ряд систем, которые довольно эффективно справлялись с нетривиальными
задачами. Примером может служить система R1/XCON, предназначенная для структурного
синтеза вычислительных систем (подробно о ней — в главе
14). В этой системе реализован ряд концепций, существенно отличающих ее как
от обычных программных приложений, так и от исследовательских программ искусственного
интеллекта (см. [Davis, 1982]). Те, которые я считаю наиболее важными,
перечислены ниже.
2.6. Машина
логического вывода и база знаний
Как правило,
в структуре экспертной системы можно четко разделить базу знаний и компонент,
который этой базой пользуется, — машину логического вывода. Взаимодействие между
ними обеспечивается программой, которую принято называть оболочкой (shell) экспертной
системы. Конечный пользователь приложения взаимодействует с системой через оболочку,
передавая ей запросы. Последняя активизирует машину логического вывода, которая
обращается к базе знаний, извлекает знания, необходимые для ответа на конкретный
вопрос, и передает сформированный ответ пользователю либо как решение проблемы,
либо в форме рекомендации или совета (рис. 2.5).
В базе данных
содержатся правила и всевозможные декларации. В частности, применительно к примеру
"Пингвин", представленному во врезке 2.5, в базе знаний, организованной
с помощью языка CLIPS, должны присутствовать следующие декларации:
(deftemplate
птица (field (тип SYMBOL)))
в дополнение
к имеющимся правилам:
(defrule (птица
(тип ?Х))
=>
(assert (да))
)
(defrule
(птица (тип
пингвин))
=>
(assert (нет))
)
Из этой декларации
следует, что объект данных птица может содержать поле (field) тип. В главе 5
вы познакомитесь с декларациями другого типа, которые служат для настройки поведения
машины логического вывода.
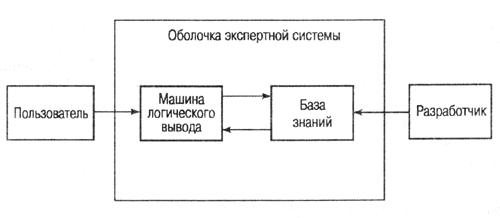
Рис. 2.5.
Структура экспертной системы
2.3.2.
Периоды "зимней спячки" и "пробуждения" в истории искусственного
интеллекта
В первой
части периода модернизма среди исследователей, занимавшихся "чистыми"
проблемами искусственного интеллекта, очень распространенным было настроение
критической самооценки. Одним из его симптомов была оживленная дискуссия между
сторонниками формальных и неформальных методов (подробнее об этом — в главе
23). Кажется само собой разумеющимся, что имеют право на существование как исследования
чисто теоретические, фундаментальные, так и прикладные, призванные использовать
фундаментальные результаты в конкретных задачах.
А тем временем
продолжалось активное развитие технологии экспертных систем для самых разных
прикладных областей. Фирмы, специализирующиеся в области искусственного интеллекта,
предлагали достаточно дорогие программные продукты, требовавшие специальной
аппаратной среды и к тому же плохо поддающиеся интеграции с другими коммерческими
системами. Вместо того чтобы осваивать свою нишу на рынке решением тех проблем,
которые восприимчивы к подходу, основанному на знаниях, делались широковещательные
заявления о создании эффективных систем, способных справиться с любой проблемой.
Возрождение
интереса к исследованиям в области искусственного интеллекта связано с новым
информационным взрывом. В расширяющейся информационной вселенной, без сомнения,
не останутся невостребованными методы искусственного интеллекта при решении,
по крайней мере, таких задач, как обработка текстов и изображений, которые нужно
извлекать из различного рода источников, анализировать, классифицировать, индексировать,
обобщать, интерпретировать и т.д. и т.п. Настало время и для внедрения результатов,
достигнутых в технологии символических вычислений и обобщенной теории представления
знаний. Но эти подходы должны сочетаться со статистическим и вероятностным подходами,
поскольку нам приходится иметь дело с огромными и все увеличивающимися объемами
информации, доступной по Internet и различным коммерческим информационным сетям.
В следующей
главе приводится описание структуры и основных принципов функционирования двух
ранних программ искусственного интеллекта. Хотя со времени создания этих систем
прошло уже более двадцати лет, они могут служить прекрасной иллюстрацией базовых
концепций, используемых при построении программ такого рода, и мне незачем извиняться
за включение этого материала в книгу. Каждую из этих программ можно рассматривать
как своеобразный мост, переброшенный между концепцией поиска в пространстве
состояний и развитием подхода, опирающегося на базы знаний. Студенты, только
приступающие к освоению материала об экспертных системах, найдут в описании
этих программ много такого, что необходимо уразуметь прежде, чем заняться более
современными системами. С последними читатель сможет поближе познакомиться в
главах 11-15 и особенно в 22 и 23, где анализируются результаты некоторых экспериментов,
демонстрирующих пределы возможностей экспертных систем.
Хорошим введением
в проблематику искусственного интеллекта могут послужить книги Рича и Найта
[Rich and Knight, 1991] и Уинстона [Winston, 1992]. Для студентов
хорошим источником ссылок на работы в этой области, хотя и несколько устаревшие
с точки зрения сегодняшнего дня, являются различные выпуски серии Handbook
of Artificial Intelligence ([Barr and Feigenbaum, 1981, 1982]; [Cohen and Feigenbaum,
1982]). Читателям, интересующимся проблемой машинного распознавания естественного
языка, рекомендую прочесть книгу Аллена (Allen, 1995), в которой описаны
фундаментальные исследования в этой области, а о том, каким видится будущее
искусственного интеллекта из окон лабораторий МИТ, читатель сможет узнать в
книге Уинстнона и Шелларда [Winston andShellard, 1990].
Начальные
главы книги Нильсона [Nilsson, 1980] по-прежнему остаются лучшим описанием
методики эвристического поиска, но более строгое математическое изложение этого
материала можно найти в работе Перла [Pearl, 1984]. Некоторые примеры
приложения методики эвристического поиска, взятые из современной практики, собраны
в сборнике [Rayward-Smith et al, 1996], а Рейард-Смит в своей книге излагает
современный взгляд на эти методы [Rayward-Smith, 1994].
Алгоритмы,
аналогичные рассмотренному А , по-прежнему привлекают немалое внимание. Например,
в одной из последних статей Корфа и Рейда [Korf and Reid, 1998] показано,
что эвристики значительно улучшают процесс поиска не тем, что сужают поиск,
как считалось до сих пор, а уменьшая его глубину. Таким образом, оказывается,
что эвристики способствуют отысканию более коротких путей решения, не снижая
при этом фактор ветвления.
1. Почему
пакет программ статистического анализа нельзя считать программой искусственного
интеллекта?
2. Могут
ли психологи подсказать нам, как сконструировать думающую машину?
3. Как вы
понимаете термин "пространство поиска"? Что представляет собой пространство
поиска в игре в шахматы?
4. Как вы
понимаете термин "пространство решений"? Что представляет собой пространство
решений в игре в шахматы?
5. Ниже приведен
алгоритм поиска в глубину. Он записан с помощью функциональной нотации, которая
подчеркивает его рекурсивную структуру. Таким образом, dfs представляет собой
функцию трех аргументов: goal, current и pending:
(а b с) + (d
e f ) = (а b с d e f);
first(a b с)
= a
rest(a b c)
= (b c).
I) Выразите
следующий алгоритм на каком-либо из известных вам языков программирования.
dfsfgoal, current,
pending)
{
if current = goal, then success;
else
{
pending := expand (current}+ pending;
if pending = () then fail;
else dfs(goal,
first(pending), .rest( pending));
} }
II) Разработайте
аналогичный алгоритм для поиска в ширину и реализуйте его на том же языке. Необходимо
будет изменить только одно выражение в функции dfs.
6. Рассмотрите
головоломку "миссионеры и каннибалы", схематически представленную
на рис. 2.6.
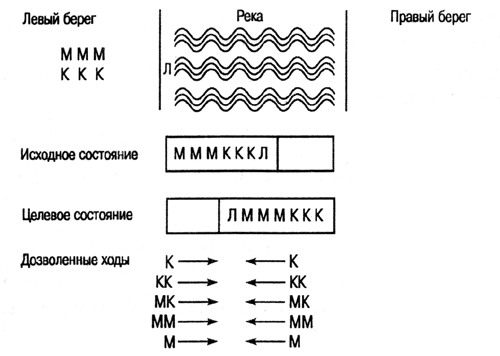
Рис. 2.6.
Головоломка "миссионеры и каннибалы "
Условия головоломки
следующие.
На левом
берегу реки находятся три миссионера и три каннибала. К этому же берегу причалена
единственная лодка. На этой лодке нужно переправить всех миссионеров и всех
каннибалов на правый берег при условии, что лодка одновременно может перевозить
не более двоих, в обратный путь на лодке должен отправиться хотя бы один человек.
Таким образом, дозволены следующие варианты шагов (переправ):
К-> одного
каннибала с левого берега на правый
КК-> двух
каннибалов с левого берега на правый
МК-> одного
миссионера и одного каннибала с левого берега на правый
ММ-> двух
миссионеров с левого берега на правый
М-> одного
миссионера с левого берега на правый
К этому нужно
добавить такие же варианты переправы с правого берега на левый. Но есть еще
одно обстоятельство, существенно влияющее на весь процесс: если окажется, что
каннибалов на любом из берегов больше, чем миссионеров, то несчастных просто
съедят. Решение головоломки — это последовательность шагов с учетом описанных
ограничений, переводящая систему в заданное конечное состояние.
Конечно,
эту головоломку можно решить и простым перебором и испытанием всех возможных
состояний, поскольку пространство поиска не так уж велико. На рис. 2.7 показано,
как образуется пространство поиска рекурсивным применением дозволенных операторов,
причем на графе состояний особо выделены узлы, приводящие к образованию петель,
и узлы, соответствующие недозволенным состояниям (когда кто-либо из миссионеров
обречен).
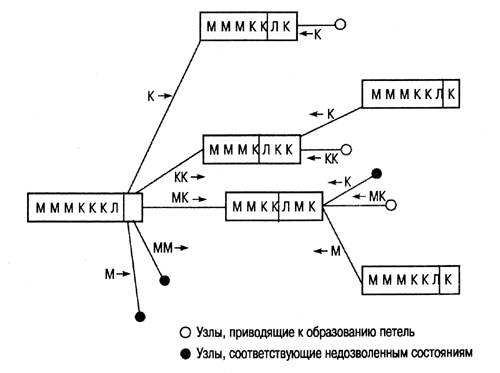
Рис. 2.7.
Построение пространства поиска в головоломке "миссионеры и каннибалы"
На рис. 2.8
показано законченное пространство поиска, сформированное алгоритмом поиска в
глубину, причем перебор возможных шагов ведется в том порядке, в котором они
перечислены в представленном в условии, списке.
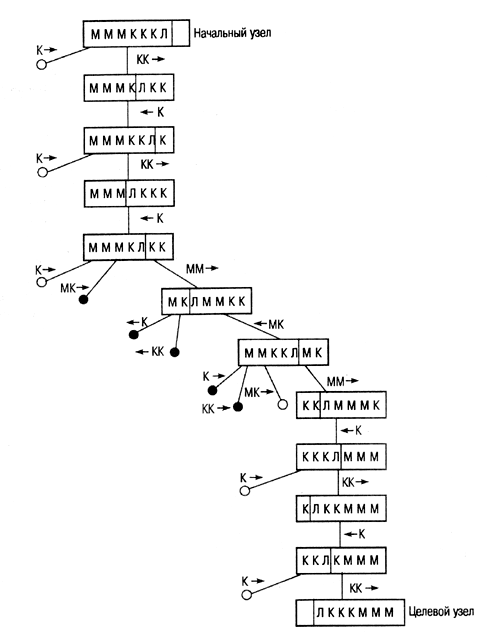
Рис. 2.8.
Законченное пространство поиска в головоломке "миссионеры и каннибалы ",
сформированное алгоритмом поиска в глубину
В процессе
поиска было развернуто 22 узла, а путь, приводящий к успеху, содержит 11 узлов.
Таким образом, оценка проницательности поиска равна 11/22=0.5. Грубо
говоря, проницательность поиска говорит нам о том, насколько данный алгоритм
позволил избежать выполнения ненужной работы в процессе Поиска решения. Чем
выше значение проницательности поиска для того или иного алгоритма, тем лучше.
I) Выберите
представление состояний на берегах реки и разработайте программу, которая решает
эту задачу, используя оба варианта алгоритмов поиска— в глубину и в ширину.
С разными способами формализации этой
задачи можно
познакомиться в работе Амарела [Amarel, 1968]. Обратите внимание на то,
что существуют способы представления состояний, которые позволяют более экономно
использовать вычислительные ресурсы при решении задачи.
II) Попытайтесь
улучшить оценку проницательности поиска, полученную для алгоритма поиска в глубину
(рис. 2.8), изменив порядок, в котором анализируются в каждом очередном состоянии
дозволенные операторы.
III) Обобщите
программу как в части количества пассажиров в лодке, так и в части количества
миссионеров/каннибалов. Сделайте их параметрами программы, задаваемыми извне.
Если вы начнете проводить эксперименты с такой программой, то убедитесь, что,
во-первых, эти параметры нельзя варьировать независимо, поскольку при некоторых
комбинациях задача не имеет решения, а во-вторых, увеличение значений любого
из параметров существенно расширяет пространство поиска.
7. Другая
классическая головоломка, знакомая в несколько ином виде многим еще со школьной
скамьи, — "Восьмерка". В головоломке принимает участие восемь пронумерованных
фишек, которые могут перемещаться по игровому полю 3x3. Цель состоит в том,
чтобы из некоторого случайного расположения фишек перейти к упорядоченному (рис.
2.9).
Мы несколько
модифицируем ограничения, сформулировав их в терминах перемещения единственного
"пустого поля".
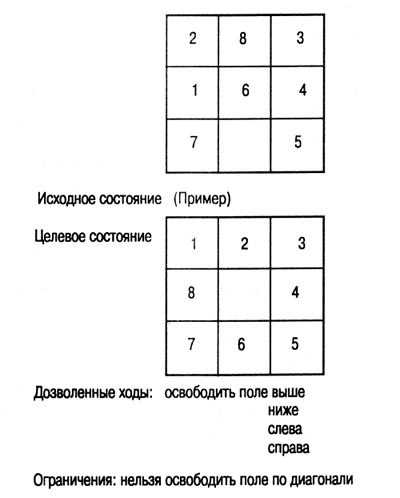
Рис. 2.9.
Головоломка "Восьмерка"
В отличие
от задачи о миссионерах и каннибалах, эту головоломку можно решить за приемлемое
время методом "слепого" поиска. Дело в том, что головоломка имеет
только 9! состояний и, следовательно, можно использовать для поиска очередного
хода оценочную функцию по методике "восхождения на гору".
I) Придумайте
оценочную функцию для этой задачи и разработайте программу, которая реализует
поиск по методике "восхождения на гору". Возможные варианты оценочной
функции некоторого состояния должны включать, во-первых, количество фишек, которые
стоят не на своих местах, а во-вторых, сумму расстояний от текущего положения
каждой фишки до предназначенного ей целевого (имеются в виду расстояния по Евклиду).
II) Какая
из предложенных выше оценочных функций является более чувствительной? Можете
ли вы предложить лучший способ управления поиском?
III) Как
будет работать ваша программа, если увеличить количество фишек до 15, а размер
игрового поля до 4x4? В этом случае придется исследовать 16! состояний.
Эту головоломку
с точки зрения методов искусственного интеллекта рассматривал Нильсон (см. [Nilsson,
1980, Chapter 1].
8. Просмотрите
описание алгоритма А во врезке 2.2 и выполните следующее.
I) Реализуйте
алгоритм А на любом известном вам языке программирования.
II) С помощью
созданной программы попробуйте решить головоломки "о миссионерах и каннибалах"
и "Восьмерку". (Придется придумать оценочную функцию для головоломки
"о миссионерах и каннибалах". Воспользуйтесь оценочной функцией из
упр. 7.)
III) Попробуйте
с помощью этого алгоритма решить криптоарифметическую головоломку, описанную
ниже:
|
BEST |
SEND |
DONALD |
CROSS |
||
|
+MADE |
+MORE |
+GERALD |
+ROADS |
||
|
MASTER |
MONEY |
ROBERT |
DANGER |
||
Термин "криптоарифметическая"
означает использование цифр, зашифрованных буквами, и соответственно чисел,
зашифрованных словами. Задача состоит в том, чтобы найти, какие цифры нужно
подставить вместо букв, чтобы представленные арифметические операции над расшифрованными
числами давали верный результат. Такая задача рассматривается во многих классических
работах по искусственному интеллекту (см., например, [Raphael, 1976, Chapter
3].
Вам придется подумать над тем, как представить слагаемые и сумму, какие возможны в решении этой задачи "ходы" (т.е. какой набор операций можно предложить для перехода из одного состояния в другое) и какую эвристику можно применить для управления поиском.